Mounted Calcite Beam Displacers
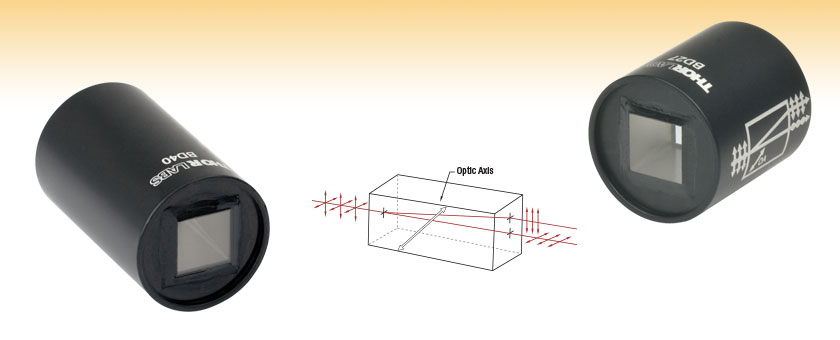
- Separate an Input into Two Orthogonally Polarized Beams
- Calcite Substrate is Transparent from 350 nm to 2.3 µm
- 2.7 mm and 4.0 mm Beam Separation Options
BD40
4.0 mm Beam Separation
BD27
2.7 mm Beam Separation
Birefringent Beam Displacers Separate Unpolarized Light into Two Orthogonally Polarized Beams

Please Wait
| Item # | BD27 | BD40 |
|---|---|---|
| Substrate | High Optical Grade Calcitea | |
| Wavelength Range (Click for Graph) |
350 nm to 2.3 µmb | |
| Damage Threshold | 20 J/cm2 (1064 nm, 10 ns, 10 Hz, Ø0.433 mm) |
|
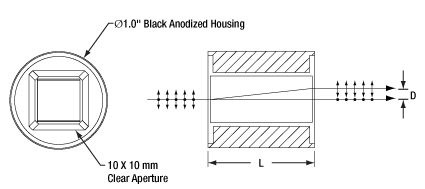
| Beam Separation (D) @ 1500 nm | 2.7 mmc | 4.0 mmc |
| Length (L) | 1.10" (2.8 cm) | 1.60" (4.1 cm) |
| Clear Aperture | 10 mm x 10 mm | |
| Beam Deviation | <30 arcsec | |
| Wavefront Distortion | <λ/4 | |
| Surface Quality | 40-20 Scratch-Dig | |
| Click on the red Document icon next to the item numbers below to access the Zemax file download. Our entire Zemax Catalog is also available. |
(6 - 8 hours).
Click to Enlarge
Figure 1.1 Schematic and Ray Diagram of Mounted Calcite Beam Displacer
Features
- Two Orthogonally Polarized Outputs
- 2.7 mm, 4.0 mm, or Custom Displacements Available
- Outputs Parallel to Input
- High Grade Optical Calcite
- 350 nm to 2.3 μm Wavelength Range
- Ø1" Housing
Beam displacing prisms are used to separate an input beam into two orthogonally polarized output beams and can be used as polarizing beamsplitters in applications where the 90° separation of the beams is not possible. Fabricated from a single piece of the highest quality optical grade calcite, our beam displacers can be used with wavelengths from 350 nm up to 2.3 μm. Since calcite is a soft crystal that can be easily damaged, our calcite polarizers are housed in a Ø1" metal housing that can be mounted into our optomechanical rotation mounts. For further information on the properties of calcite, please see the Calcite tab.
Our mounted beam displacers are offered in two versions, which provide a beam displacement of either 2.7 mm or 4.0 mm. In both versions both output beams are parallel to the input beam to within 30 arcsec. We also offer calcite beam displacer modules for our FiberBench systems, available here.
Please note that the beam displacing prism is epoxied within the mount and cannot be removed. Please contact Tech Support for an unmounted version of the calcite beam displacer.
| Birefringent Crystal Beamsplitters | ||
|---|---|---|
| Type | Ordinary Ray Anglea | Extraordinary Ray Anglea |
| Calcite Beam Displacers | Parallel | Parallel |
| YVO4 Beam Displacers | ||
| Rochon Prisms | Parallel | Deviated |
| Wollaston Prisms | Deviated | Deviated |
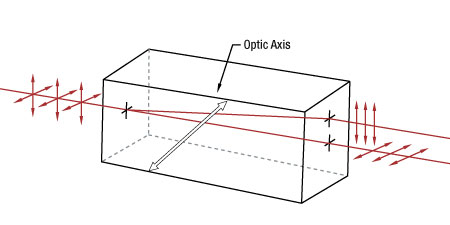
Figure 2.1 Polarization-Dependent Refraction - Calcite Beam Displacer
Our calcite polarization-dependent beam displacers are based on high-grade, birefringent calcite crystals. Due to the birefringent nature of calcite, waves polarized in the direction of the optic axis propagate with a different index of refraction than waves polarized orthogonally to the optic axis. In our beam displacers, this birefringence laterally separates the two orthogonal polarization states of an incident beam. When unpolarized light is normally incident on the optic, ordinary rays travel straight through the crystal while extraordinary rays exit the crystal displaced by a distance that depends on the light's wavelength and the length of the crystal.
A calcite beam displacing polarizer is used to separate the orthogonally-polarized components of a beam. Our calcite beam displacers are composed of single rectangular mounted calcite prisms (shown in Figure 2.1). The length of these prisms has been chosen to separate the beams by 2.7 mm or 4.0 mm. Since calcite is a soft crystal that is easily damaged, almost all of our calcite polarizers are offered in metal housings. With convenient threadings and adapters, these housings can easily be mounted into our opto-mechanical products.
| Thorlabs' Calcite Polarizers | ||
|---|---|---|
| Glan-Laser Polarizers | Glan-Taylor Polarizers | Wollaston Polarizers |
| Mounted Glan-Thompson Polarizers Unmounted Glan-Thompson Polarizers |
Double Glan-Taylor Polarizer | Beam Displacers |

Figure 3.2 Lens Tube Fixed to PRM1 Mount

Figure 3.1 Thread Lens Tube into PRM1 Mount

Figure 3.4 Secure the Beam Displacer in the Mount with a Spanner Wrench

Figure 3.3 Insert the Beam Displacer in the Lens Tube
Beam Displacer Mounting
Thorlabs Calcite Beam Displacers can be mounted to a PRM1 rotation mount by using a SM1L20 lens tube:
- Remove the SM1RR retaining ring that comes with the PRM1 rotation mount.
- Screw the threaded end of the lens tube into the rotation mount as shown in Figure 3.1.
- Once the lens tube is threaded (Figure 3.2), insert the mounted beam displacer into the other end of the lens tube (see Figure 3.3)
- Secure the beam displacer into place using the retaining ring included with the lens tube.
- A SPW602 spanner wrench can be used to tighten the retaining ring (Figure 3.4).
Note: The SM1P1 Ø1" to SM1 adapter can be used in place of the SM1L20 lens tube when space is not available for the extra length of the lens tube.
Laser Induced Damage Threshold Tutorial
The following is a general overview of how laser induced damage thresholds are measured and how the values may be utilized in determining the appropriateness of an optic for a given application. When choosing optics, it is important to understand the Laser Induced Damage Threshold (LIDT) of the optics being used. The LIDT for an optic greatly depends on the type of laser you are using. Continuous wave (CW) lasers typically cause damage from thermal effects (absorption either in the coating or in the substrate). Pulsed lasers, on the other hand, often strip electrons from the lattice structure of an optic before causing thermal damage. Note that the guideline presented here assumes room temperature operation and optics in new condition (i.e., within scratch-dig spec, surface free of contamination, etc.). Because dust or other particles on the surface of an optic can cause damage at lower thresholds, we recommend keeping surfaces clean and free of debris. For more information on cleaning optics, please see our Optics Cleaning tutorial.
Testing Method
Thorlabs' LIDT testing is done in compliance with ISO/DIS 11254 and ISO 21254 specifications.
First, a low-power/energy beam is directed to the optic under test. The optic is exposed in 10 locations to this laser beam for 30 seconds (CW) or for a number of pulses (pulse repetition frequency specified). After exposure, the optic is examined by a microscope (~100X magnification) for any visible damage. The number of locations that are damaged at a particular power/energy level is recorded. Next, the power/energy is either increased or decreased and the optic is exposed at 10 new locations. This process is repeated until damage is observed. The damage threshold is then assigned to be the highest power/energy that the optic can withstand without causing damage. A histogram such as that below represents the testing of one BB1-E02 mirror.

The photograph above is a protected aluminum-coated mirror after LIDT testing. In this particular test, it handled 0.43 J/cm2 (1064 nm, 10 ns pulse, 10 Hz, Ø1.000 mm) before damage.
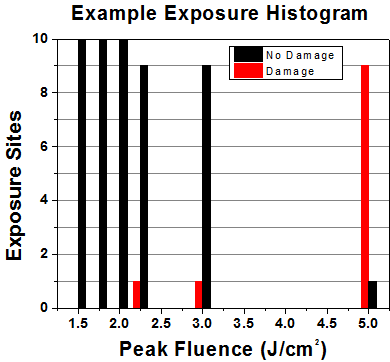
| Example Test Data | |||
|---|---|---|---|
| Fluence | # of Tested Locations | Locations with Damage | Locations Without Damage |
| 1.50 J/cm2 | 10 | 0 | 10 |
| 1.75 J/cm2 | 10 | 0 | 10 |
| 2.00 J/cm2 | 10 | 0 | 10 |
| 2.25 J/cm2 | 10 | 1 | 9 |
| 3.00 J/cm2 | 10 | 1 | 9 |
| 5.00 J/cm2 | 10 | 9 | 1 |
According to the test, the damage threshold of the mirror was 2.00 J/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.803 mm). Please keep in mind that these tests are performed on clean optics, as dirt and contamination can significantly lower the damage threshold of a component. While the test results are only representative of one coating run, Thorlabs specifies damage threshold values that account for coating variances.
Continuous Wave and Long-Pulse Lasers
When an optic is damaged by a continuous wave (CW) laser, it is usually due to the melting of the surface as a result of absorbing the laser's energy or damage to the optical coating (antireflection) [1]. Pulsed lasers with pulse lengths longer than 1 µs can be treated as CW lasers for LIDT discussions.
When pulse lengths are between 1 ns and 1 µs, laser-induced damage can occur either because of absorption or a dielectric breakdown (therefore, a user must check both CW and pulsed LIDT). Absorption is either due to an intrinsic property of the optic or due to surface irregularities; thus LIDT values are only valid for optics meeting or exceeding the surface quality specifications given by a manufacturer. While many optics can handle high power CW lasers, cemented (e.g., achromatic doublets) or highly absorptive (e.g., ND filters) optics tend to have lower CW damage thresholds. These lower thresholds are due to absorption or scattering in the cement or metal coating.

LIDT in linear power density vs. pulse length and spot size. For long pulses to CW, linear power density becomes a constant with spot size. This graph was obtained from [1].
Pulsed lasers with high pulse repetition frequencies (PRF) may behave similarly to CW beams. Unfortunately, this is highly dependent on factors such as absorption and thermal diffusivity, so there is no reliable method for determining when a high PRF laser will damage an optic due to thermal effects. For beams with a high PRF both the average and peak powers must be compared to the equivalent CW power. Additionally, for highly transparent materials, there is little to no drop in the LIDT with increasing PRF.
In order to use the specified CW damage threshold of an optic, it is necessary to know the following:
- Wavelength of your laser
- Beam diameter of your beam (1/e2)
- Approximate intensity profile of your beam (e.g., Gaussian)
- Linear power density of your beam (total power divided by 1/e2 beam diameter)
Thorlabs expresses LIDT for CW lasers as a linear power density measured in W/cm. In this regime, the LIDT given as a linear power density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size, as demonstrated by the graph to the right. Average linear power density can be calculated using the equation below.
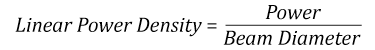
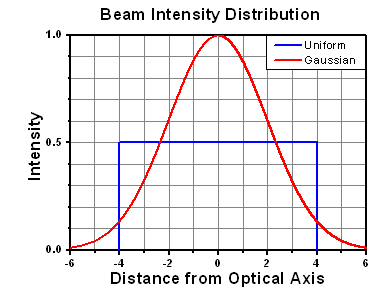
The calculation above assumes a uniform beam intensity profile. You must now consider hotspots in the beam or other non-uniform intensity profiles and roughly calculate a maximum power density. For reference, a Gaussian beam typically has a maximum power density that is twice that of the uniform beam (see lower right).
Now compare the maximum power density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately. A good rule of thumb is that the damage threshold has a linear relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 10 W/cm at 1310 nm scales to 5 W/cm at 655 nm):

While this rule of thumb provides a general trend, it is not a quantitative analysis of LIDT vs wavelength. In CW applications, for instance, damage scales more strongly with absorption in the coating and substrate, which does not necessarily scale well with wavelength. While the above procedure provides a good rule of thumb for LIDT values, please contact Tech Support if your wavelength is different from the specified LIDT wavelength. If your power density is less than the adjusted LIDT of the optic, then the optic should work for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. The damage analysis will be carried out on a similar optic (customer's optic will not be damaged). Testing may result in additional costs or lead times. Contact Tech Support for more information.
Pulsed Lasers
As previously stated, pulsed lasers typically induce a different type of damage to the optic than CW lasers. Pulsed lasers often do not heat the optic enough to damage it; instead, pulsed lasers produce strong electric fields capable of inducing dielectric breakdown in the material. Unfortunately, it can be very difficult to compare the LIDT specification of an optic to your laser. There are multiple regimes in which a pulsed laser can damage an optic and this is based on the laser's pulse length. The highlighted columns in the table below outline the relevant pulse lengths for our specified LIDT values.
Pulses shorter than 10-9 s cannot be compared to our specified LIDT values with much reliability. In this ultra-short-pulse regime various mechanics, such as multiphoton-avalanche ionization, take over as the predominate damage mechanism [2]. In contrast, pulses between 10-7 s and 10-4 s may cause damage to an optic either because of dielectric breakdown or thermal effects. This means that both CW and pulsed damage thresholds must be compared to the laser beam to determine whether the optic is suitable for your application.
| Pulse Duration | t < 10-9 s | 10-9 < t < 10-7 s | 10-7 < t < 10-4 s | t > 10-4 s |
|---|---|---|---|---|
| Damage Mechanism | Avalanche Ionization | Dielectric Breakdown | Dielectric Breakdown or Thermal | Thermal |
| Relevant Damage Specification | No Comparison (See Above) | Pulsed | Pulsed and CW | CW |
When comparing an LIDT specified for a pulsed laser to your laser, it is essential to know the following:
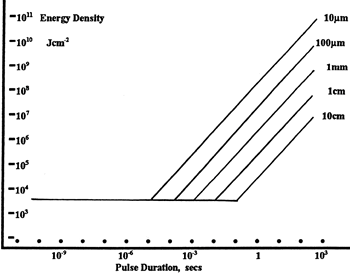
LIDT in energy density vs. pulse length and spot size. For short pulses, energy density becomes a constant with spot size. This graph was obtained from [1].
- Wavelength of your laser
- Energy density of your beam (total energy divided by 1/e2 area)
- Pulse length of your laser
- Pulse repetition frequency (prf) of your laser
- Beam diameter of your laser (1/e2 )
- Approximate intensity profile of your beam (e.g., Gaussian)
The energy density of your beam should be calculated in terms of J/cm2. The graph to the right shows why expressing the LIDT as an energy density provides the best metric for short pulse sources. In this regime, the LIDT given as an energy density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size. This calculation assumes a uniform beam intensity profile. You must now adjust this energy density to account for hotspots or other nonuniform intensity profiles and roughly calculate a maximum energy density. For reference a Gaussian beam typically has a maximum energy density that is twice that of the 1/e2 beam.
Now compare the maximum energy density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately [3]. A good rule of thumb is that the damage threshold has an inverse square root relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 1 J/cm2 at 1064 nm scales to 0.7 J/cm2 at 532 nm):
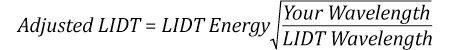
You now have a wavelength-adjusted energy density, which you will use in the following step.
Beam diameter is also important to know when comparing damage thresholds. While the LIDT, when expressed in units of J/cm², scales independently of spot size; large beam sizes are more likely to illuminate a larger number of defects which can lead to greater variances in the LIDT [4]. For data presented here, a <1 mm beam size was used to measure the LIDT. For beams sizes greater than 5 mm, the LIDT (J/cm2) will not scale independently of beam diameter due to the larger size beam exposing more defects.
The pulse length must now be compensated for. The longer the pulse duration, the more energy the optic can handle. For pulse widths between 1 - 100 ns, an approximation is as follows:
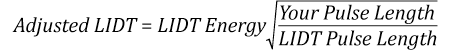
Use this formula to calculate the Adjusted LIDT for an optic based on your pulse length. If your maximum energy density is less than this adjusted LIDT maximum energy density, then the optic should be suitable for your application. Keep in mind that this calculation is only used for pulses between 10-9 s and 10-7 s. For pulses between 10-7 s and 10-4 s, the CW LIDT must also be checked before deeming the optic appropriate for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. Contact Tech Support for more information.
[1] R. M. Wood, Optics and Laser Tech. 29, 517 (1998).
[2] Roger M. Wood, Laser-Induced Damage of Optical Materials (Institute of Physics Publishing, Philadelphia, PA, 2003).
[3] C. W. Carr et al., Phys. Rev. Lett. 91, 127402 (2003).
[4] N. Bloembergen, Appl. Opt. 12, 661 (1973).
In order to illustrate the process of determining whether a given laser system will damage an optic, a number of example calculations of laser induced damage threshold are given below. For assistance with performing similar calculations, we provide a spreadsheet calculator that can be downloaded by clicking the LIDT Calculator button. To use the calculator, enter the specified LIDT value of the optic under consideration and the relevant parameters of your laser system in the green boxes. The spreadsheet will then calculate a linear power density for CW and pulsed systems, as well as an energy density value for pulsed systems. These values are used to calculate adjusted, scaled LIDT values for the optics based on accepted scaling laws. This calculator assumes a Gaussian beam profile, so a correction factor must be introduced for other beam shapes (uniform, etc.). The LIDT scaling laws are determined from empirical relationships; their accuracy is not guaranteed. Remember that absorption by optics or coatings can significantly reduce LIDT in some spectral regions. These LIDT values are not valid for ultrashort pulses less than one nanosecond in duration.

Figure 71A A Gaussian beam profile has about twice the maximum intensity of a uniform beam profile.
CW Laser Example
Suppose that a CW laser system at 1319 nm produces a 0.5 W Gaussian beam that has a 1/e2 diameter of 10 mm. A naive calculation of the average linear power density of this beam would yield a value of 0.5 W/cm, given by the total power divided by the beam diameter:
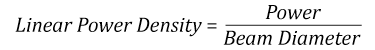
However, the maximum power density of a Gaussian beam is about twice the maximum power density of a uniform beam, as shown in Figure 71A. Therefore, a more accurate determination of the maximum linear power density of the system is 1 W/cm.
An AC127-030-C achromatic doublet lens has a specified CW LIDT of 350 W/cm, as tested at 1550 nm. CW damage threshold values typically scale directly with the wavelength of the laser source, so this yields an adjusted LIDT value:

The adjusted LIDT value of 350 W/cm x (1319 nm / 1550 nm) = 298 W/cm is significantly higher than the calculated maximum linear power density of the laser system, so it would be safe to use this doublet lens for this application.
Pulsed Nanosecond Laser Example: Scaling for Different Pulse Durations
Suppose that a pulsed Nd:YAG laser system is frequency tripled to produce a 10 Hz output, consisting of 2 ns output pulses at 355 nm, each with 1 J of energy, in a Gaussian beam with a 1.9 cm beam diameter (1/e2). The average energy density of each pulse is found by dividing the pulse energy by the beam area:
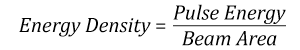
As described above, the maximum energy density of a Gaussian beam is about twice the average energy density. So, the maximum energy density of this beam is ~0.7 J/cm2.
The energy density of the beam can be compared to the LIDT values of 1 J/cm2 and 3.5 J/cm2 for a BB1-E01 broadband dielectric mirror and an NB1-K08 Nd:YAG laser line mirror, respectively. Both of these LIDT values, while measured at 355 nm, were determined with a 10 ns pulsed laser at 10 Hz. Therefore, an adjustment must be applied for the shorter pulse duration of the system under consideration. As described on the previous tab, LIDT values in the nanosecond pulse regime scale with the square root of the laser pulse duration:
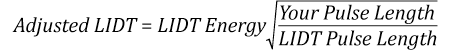
This adjustment factor results in LIDT values of 0.45 J/cm2 for the BB1-E01 broadband mirror and 1.6 J/cm2 for the Nd:YAG laser line mirror, which are to be compared with the 0.7 J/cm2 maximum energy density of the beam. While the broadband mirror would likely be damaged by the laser, the more specialized laser line mirror is appropriate for use with this system.
Pulsed Nanosecond Laser Example: Scaling for Different Wavelengths
Suppose that a pulsed laser system emits 10 ns pulses at 2.5 Hz, each with 100 mJ of energy at 1064 nm in a 16 mm diameter beam (1/e2) that must be attenuated with a neutral density filter. For a Gaussian output, these specifications result in a maximum energy density of 0.1 J/cm2. The damage threshold of an NDUV10A Ø25 mm, OD 1.0, reflective neutral density filter is 0.05 J/cm2 for 10 ns pulses at 355 nm, while the damage threshold of the similar NE10A absorptive filter is 10 J/cm2 for 10 ns pulses at 532 nm. As described on the previous tab, the LIDT value of an optic scales with the square root of the wavelength in the nanosecond pulse regime:
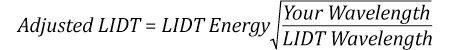
This scaling gives adjusted LIDT values of 0.08 J/cm2 for the reflective filter and 14 J/cm2 for the absorptive filter. In this case, the absorptive filter is the best choice in order to avoid optical damage.
Pulsed Microsecond Laser Example
Consider a laser system that produces 1 µs pulses, each containing 150 µJ of energy at a repetition rate of 50 kHz, resulting in a relatively high duty cycle of 5%. This system falls somewhere between the regimes of CW and pulsed laser induced damage, and could potentially damage an optic by mechanisms associated with either regime. As a result, both CW and pulsed LIDT values must be compared to the properties of the laser system to ensure safe operation.
If this relatively long-pulse laser emits a Gaussian 12.7 mm diameter beam (1/e2) at 980 nm, then the resulting output has a linear power density of 5.9 W/cm and an energy density of 1.2 x 10-4 J/cm2 per pulse. This can be compared to the LIDT values for a WPQ10E-980 polymer zero-order quarter-wave plate, which are 5 W/cm for CW radiation at 810 nm and 5 J/cm2 for a 10 ns pulse at 810 nm. As before, the CW LIDT of the optic scales linearly with the laser wavelength, resulting in an adjusted CW value of 6 W/cm at 980 nm. On the other hand, the pulsed LIDT scales with the square root of the laser wavelength and the square root of the pulse duration, resulting in an adjusted value of 55 J/cm2 for a 1 µs pulse at 980 nm. The pulsed LIDT of the optic is significantly greater than the energy density of the laser pulse, so individual pulses will not damage the wave plate. However, the large average linear power density of the laser system may cause thermal damage to the optic, much like a high-power CW beam.
| Posted Comments: | |
Siddharth Sivankutty
(posted 2025-04-15 11:41:57.067) Dear Thorlabs team,
Do you have information on the relative group delay between the o- and e- ray for the BD-27 and the BD-40, say at 1030 nm ? EGies
(posted 2025-04-18 06:44:03.0) Thank you for contacting Thorlabs. There is about 20 ps of group delay between the o-ray and the e-ray for the BD40, and about 15 ps for the BD27. I have reached out to you directly regarding this. Philipp Rößner
(posted 2022-11-04 14:21:08.623) Is it possible to get a Calcite Beam Displacer, 2.7 mm Beam Separation unmounted, but with Antireflective coating?
Thank you
Best regards
Philipp Raviv Ilani
(posted 2022-09-08 19:06:18.853) Can you provide me with a quote for a beam separation of 0.050 mm (50 micrometers)? cdolbashian
(posted 2022-09-26 04:55:58.0) Unfortunately, creating a calcite beam displacer with 50um separation would be a bit unfeasible given the necessary thickness of the component. I have contacted you directly to discuss other alternatives to your displacement needs. Christian Marciniak
(posted 2020-06-02 12:18:01.757) Greetings,
can I assume the PER to be in the 1:10,000 - 1:100,000 region on both beams?
Cheers YLohia
(posted 2020-06-03 02:05:23.0) Hello Christian, thank you for contacting Thorlabs. Yes, that polarization extinction ratio is a reasonable assumption, as long as you are able to pick off both beams. user
(posted 2019-02-12 18:47:32.527) Hi, I'd like to know the angle of the optical axis to the horizontal plane. nbayconich
(posted 2019-03-15 09:06:34.0) Thank you for contacting Thorlabs. The calcite's optical axis is 45 degrees with respect to the horizontal plane. user
(posted 2018-02-03 04:35:23.76) Hello, I would like to know the refractive index of BD27 at 632.5nm wavelength. tcampbell
(posted 2018-02-05 09:11:14.0) Hello, thank you for contacting Thorlabs. You can find information on the refractive index on our substrates page, including a graph of the index of refraction vs. wavelength, as well as the Sellmeier equations for the ordinary and extraordinary rays. The link to the page is here: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=6973&tabname=Calcite parksj003
(posted 2017-01-16 23:32:51.307) Hello,
I am looking for the beam displacing prisms that will be placed beween the focusing lens (focal length is ~ 200mm) and the CCD camera; different polarization of the beam would focused in the different location in the CCD plane simultaneously. Do you think there is no problem? If so, would you recommend the proper beam displacing prisms for us?
*the wavelength of the beam is 500-600 nm.
*The beam size that impinges on the beam displacing prism is about 3 mm.
Best,
Seongjun tfrisch
(posted 2017-02-17 10:55:22.0) Hello, thank you for contacting Thorlabs. I will reach out to you directly about the details of your application and what image you are looking to produce. angervax
(posted 2016-07-22 10:57:45.59) Dear Sir/Madam!
Is it possible to use Calcite Beam Displacer at 325 nm wavelength? And could the output beams be made unparallel? Thank You! nick
(posted 2015-05-12 18:02:26.93) Can you provide me with a quote for a beam separation of 0.050 mm (50 micrometers)? besembeson
(posted 2015-07-15 10:55:53.0) Response from Bweh at Thorlabs USA: I will followup with you by email regarding quoting this. This may be very thin. carlos.macias
(posted 2015-01-26 12:07:26.21) Is it possible to put an anti-relfection coating on the entry and exit faces? jlow
(posted 2015-02-03 10:19:23.0) Response from Jeremy at Thorlabs: We can put AR coating on this. We will contact you directly for details. IGKIOU
(posted 2014-10-07 04:34:46.203) Hi, how is the prism fixed on the mount? Is it possible to remove the prism from the mount? jlow
(posted 2014-10-08 04:12:06.0) Response from Jeremy at Thorlabs: The prism is epoxied in the Ø1" mount and it is not possible to remove it. user
(posted 2013-07-18 09:37:28.1) I'd like to know the approx. damage threshold of BD27 & Bd40. Is it comparable to GL10??? pbui
(posted 2013-07-18 16:30:00.0) Response from Phong at Thorlabs: Yes, the damage threshold of BD27 and BD40 would be similar to the GL10. Uncoated calcite has a damage threshold of about 500W/cm^2. We will contact you directly to discuss this further. user
(posted 2013-04-15 18:08:02.91) Can you please tell me the refractive index of the BD27 prism? jlow
(posted 2013-04-16 12:11:00.0) Response from Jeremy at Thorlabs: At 1.5µm, the ordinary refractive index is around 1.63457 and for the extraordinary, it is around 1.47743. tcohen
(posted 2012-05-04 15:59:00.0) Response from Tim at Thorlabs: Thank you for your feedback! There was a discrepancy between the specified wavefront distortion found on our Wollaston Prism family page and the individual product drawings. The correct specification is lambda/4, the same as these calcite beam displacers. We will update the web presentation to reflect this information. ahambi
(posted 2012-05-02 08:02:55.0) Dear Sirs, We are interested in receiving info on your microlens arrays. Two of the most important data we need to know is the concentration of the microlenses and their focal length. I look forward to receiving your feedback. With best regards, tcohen
(posted 2012-02-29 10:55:00.0) Response from Tim at Thorlabs: Thank you for your feedback. The calcite crystal in the BD27 is 26.8mm +/- .12mm. In the BD40 it is 39.7mm +/- .12mm. user
(posted 2012-02-29 06:50:24.0) What are the tolerances for the length of the calcite crystals? bdada
(posted 2011-03-04 19:06:00.0) Response from Buki:
Yes, the beam displacers are bidirectional and can be used as either a polarization splitter/combiner or as a polarizer element that removes the angled, orthogonally polarized component of a beam. However, the minimal beam separation we offer is 2.7mm for BD27. The beam displacers are not AR coated, but we can offer custom versions with a coating. shrotriy
(posted 2011-03-04 12:55:06.0) Are the beam displacer bidirectional i. e. can these also be used to combine the beams. we are interested in a beam displacer with 2mm or 1mm beam separation to used with HeNe laser (633 nm). Is there anti-reflective coating. Thorlabs
(posted 2010-07-26 10:54:23.0) Response from Javier at Thorlabs to acer.su: Thank you for your feedback. We can quote a shorter version of these beam displacers that yields a beam separation of 1.5 mm. I will contact you directly for quoatation details. acer.su
(posted 2010-07-26 05:52:14.0) My special requirement is output beam "D" is under 1.5 mm , would you pls check the possibility solution . |
Polarizer Selection Guide
Thorlabs offers a diverse range of polarizers, including wire grid, film, calcite, alpha-BBO, rutile, and beamsplitting polarizers. Collectively, our line of wire grid polarizers offers coverage from the visible range to the beginning of the Far-IR range. Our nanoparticle linear film polarizers provide extinction ratios as high as 100 000:1. Alternatively, our other film polarizers offer an affordable solution for polarizing light from the visible to the Near-IR. Next, our beamsplitting polarizers allow for use of the reflected beam, as well as the more completely polarized transmitted beam. Finally, our alpha-BBO (UV), calcite (visible to Near-IR), rutile (Near-IR to Mid-IR), and yttrium orthovanadate (YVO4) (Near-IR to Mid-IR) polarizers each offer an exceptional extinction ratio of 100 000:1 within their respective wavelength ranges.
To explore the available types, wavelength ranges, extinction ratios, transmission, and available sizes for each polarizer category, click More [+] in the appropriate row below.
| Wire Grid Polarizers |
|---|
| Film Polarizers |
|---|
| Beamsplitting Polarizers |
|---|
| alpha-BBO Polarizers |
|---|
| Calcite Polarizers |
|---|
| Quartz Polarizers |
|---|
| Magnesium Fluoride Polarizers |
|---|
| Yttrium Orthovanadate (YVO4) Polarizers |
|---|
| Rutile Polarizers |
|---|
 Products Home
Products Home










 Calcite Beam Displacers
Calcite Beam Displacers