Microscope Objectives, Water Dipping or Immersion

- Especially Suited for Multiphoton Imaging
- Numerical Aperture Options: 0.30 to 1.15
- Working Distance Options: 0.59 to 5.5 mm
- Options for UV to NIR Wavelengths
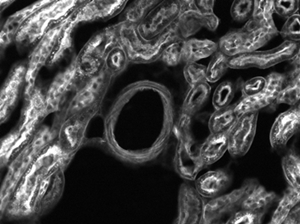
Dendridic Spine Image Collected with the N60X-NIR Objective at a Laser Wavelength of 1040 nmb
TL20X-MPL
0.6 NA, 5.5 mm WD
N25X-APO-MP
1.1 NA, 2.0 mm WD
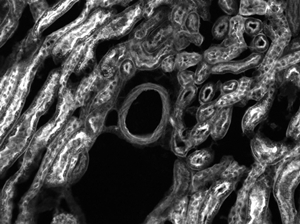
Deep Tissue Imaging of Mouse Embryo Section with the N20X-PFH Objectivea
N20X-PFH
1.0 NA, 2.0 mm WD
N16XLWD-PF
0.8 NA, 3.0 mm WD
a. This mouse embryo sample is courtesy of Dr. Rieko Ajima, National Cancer Institute, Frederick, MD.
b. This dendritic spine image is courtesy of Dr. Tobias Rose, Max Planck Institute for Neurobiology, Martinsreid, Germany.

Please Wait
| Objective Lens Selection Guide |
|---|
| Objectives |
| Super Apochromatic Microscope Objectives Microscopy Objectives, Dry Microscopy Objectives, Oil Immersion Physiology Objectives, Water Dipping or Immersion Phase Contrast Objectives Long Working Distance Objectives Reflective Microscopy Objectives UV Focusing Objectives VIS and NIR Focusing Objectives |
| Scan Lenses and Tube Lenses |
| Scan Lenses F-Theta Scan Lenses Infinity-Corrected Tube Lenses |

Did You Know?
Multiple optical elements, including the microscope objective, tube lens, and eyepieces, together define the magnification of a system. See the Magnification & FOV tab to learn more.
Click for Details
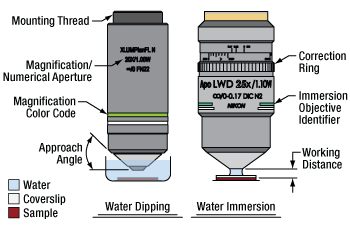
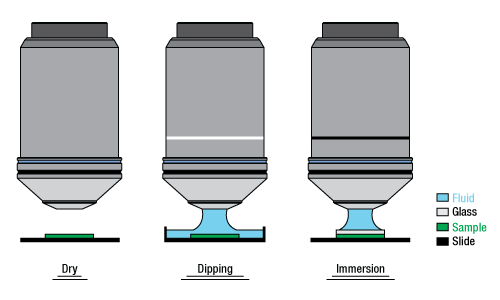
Examples of Water Dipping and Water Immersion Designs
(See Objective Tutorial Tab for More Information About Microscope Objective Types)
Features
- High Numerical Apertures with Long Working Distances
- Infinity-Corrected Apochromatic or Plan Fluorite Designs
Thorlabs offers a selection of water dipping and water immersion objectives at several magnifications that are designed for physiology applications. With high performance across broad spectral ranges, these objectives are especially suitable for transmitting excitation and emmission signals in multiphoton microscopy and other imaging techniques used for life science. The apochromatic and plan fluorite objectives sold below are corrected for chromatic aberrations at multiple wavelengths to provide sharp focus across wavelength ranges from the UV to NIR.
The long working distances (WD) and steep approach angles at the tips of these objectives provide ample space for additional optics or tools such as micromanipulators often used in electrophysiology. The high numerical apertures (NA) of these objectives allow for excitation light to be focused to a small volume, which leads to better axial and lateral resolution. For signal collection, the high NA helps to maximize intensity by capturing photons that are scattered through tissue.
Each water dipping objective is intended to be used without a coverslip (cover glass) and with the tip of the objective dipped into water surrounding the sample, either creating a meniscus or completely submerged. Water immersion objectives should be used with a coverslip that has a drop of water on top to create a meniscus between the objective tip and coverslip. The N25X-APO-MP and N25X-APO-MP1300 objectives have a correction collar that allows them to be used either with or without a coverslip. The diagram above provides a description of typical features on water dipping and immersion objectives.
These objectives feature M25 x 0.75 or M32 x 0.75 threading and 60 mm or 75 mm parfocal lengths. To use these objectives with a different thread standard, please see our microscope objective thread adapters. Thorlabs also offers a PLE153 Parfocal Length Extender for increasing the parfocal length of objectives with M25 x 0.75 threading from 60 mm to 75 mm.
| Magnification | 10X | 16X | 20X | 25X | 40X | 60X | |||
|---|---|---|---|---|---|---|---|---|---|
| Item # | N10XW-PF | N16XLWD-PF | TL20X-MPL | N20X-PFH | N25X-APO-MP | N25X-APO-MP1300 | N40XLWD-NIR | N40X-NIR | N60X-NIR |
| Manufacturer | Nikon | Thorlabs | Olympus | Nikon | |||||
| Manufacturer Part # | MRH07120 | MRP07220 | TL20X-MPL | 1-U2B965 | MRD77220 | MRD77225 | MRD77410 | MRD07420 | MRD07620 |
| Objective Class | Plan Fluorite | Plan Fluorite | Apochromat | Plan Fluorite | Apochromat | Apochromat | Apochromat | Apochromat | Apochromat |
| Numerical Aperture (NA) | 0.30 | 0.80 | 0.60 | 1.00 | 1.10 | 1.15 | 0.80 | 1.00 | |
| Effective Focal Length (EFL) | 20 mm | 12.5 mm | 10.0 mm | 9.0 mm | 8.0 mm | 5.0 mm | 5.0 mm | 3.3 mm | |
| Entrance Pupila | Ø12 mm | Ø20.0 mm | Ø12 mm | Ø18 mm | Ø17.6 mm | Ø11.5 mm | Ø8.0 mm | Ø6.7 mm | |
| Working Distance | 3.5 mm | 3.0 mm | 5.5 mm | 2.00 mm | 2.0 mm | 0.59 - 0.61 mm | 3.5 mm | 2.8 mm | |
| Resolutionb | 1.1 µm | 0.4 µm | 0.6 µm | 0.3 µm | 0.3 µm | 0.3 µm | 0.4 µm | 0.3 µm | |
| Parfocal Length | 60 mm | 75 mm | 58.4 mm | 75 mm | 75 mm | 60 mm | |||
| Design Tube Lens Focal Lengthc | 200 mm | 180 mm | 200 mm | ||||||
| Coverslip Correctiond | N/A | 0 - 0.17 mm | 0.15 - 0.19 mm | N/A | |||||
| Immersion | Water Dipping | Water Dipping or Water Immersion (Coverslip) |
Water Immersion (Coverslip) | Water Dipping | |||||
| Wavelength Range | 360 - 1500 nm | 380 - 1100 nm | 400 - 900 nm | 400 - 900 nm | 380 - 1050 nm | 420 - 1400 nm | 360 - 1100 nm | 380 - 1100 nm | 380 - 1100 nm |
| Threading | M25 x 0.75 | M32 x 0.75 | M25 x 0.75 | M25 x 0.75 | M32 x 0.75 | M25 x 0.75 | |||
| Thread Depth | 5.1 mm | 5.0 mm | 3.6 mm | 5.8 mm | 4.7 mm | 5.1 mm | |||
| Temperature Rangee | -18 - 60 °C (0 - 140 °F) | N/A | -18 - 60 °C (0 - 140 °F) | ||||||
| Chromatic Aberration Correction per ISO Standard 19012-2 | ||
|---|---|---|
| Objective Class | Common Abbreviations | Axial Focal Shift Tolerancesa |
| Achromat | ACH, ACHRO, ACHROMAT | |δC' - δF'| ≤ 2 x δob |
| Semiapochromat (or Fluorite) |
SEMIAPO, FL, FLU | |δC' - δF'| ≤ 2 x δob |δF' - δe| ≤ 2.5 x δob |δC' - δe| ≤ 2.5 x δob |
| Apochromat | APO | |δC' - δF'| ≤ 2 x δob |δF' - δe| ≤ δob |δC' - δe| ≤ δob |
| Super Apochromat | SAPO | See Footnote b |
| Improved Visible Apochromat | VIS+ | See Footnotes b and c |
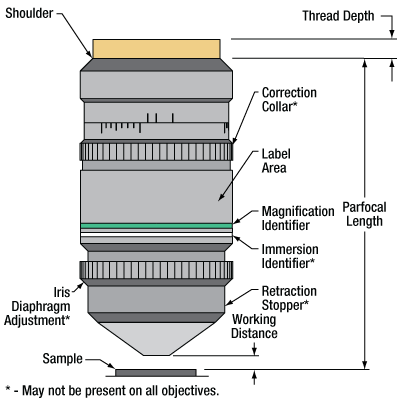
Parts of a Microscope Objective
Click on each label for more details.
This microscope objective serves only as an example. The features noted above with an asterisk may not be present on all objectives; they may be added, relocated, or removed from objectives based on the part's needs and intended application space.
Objective Tutorial
This tutorial describes features and markings of objectives and what they tell users about an objective's performance.
Objective Class and Aberration Correction
Objectives are commonly divided by their class. An objective's class creates a shorthand for users to know how the objective is corrected for imaging aberrations. There are two types of aberration corrections that are specified by objective class: field curvature and chromatic aberration.
Field curvature (or Petzval curvature) describes the case where an objective's plane of focus is a curved spherical surface. This aberration makes widefield imaging or laser scanning difficult, as the corners of an image will fall out of focus when focusing on the center. If an objective's class begins with "Plan", it will be corrected to have a flat plane of focus.
Images can also exhibit chromatic aberrations, where colors originating from one point are not focused to a single point. To strike a balance between an objective's performance and the complexity of its design, some objectives are corrected for these aberrations at a finite number of target wavelengths.
Five objective classes are shown in the table to the right; only three common objective classes are defined under the International Organization for Standards ISO 19012-2: Microscopes -- Designation of Microscope Objectives -- Chromatic Correction. Due to the need for better performance, we have added two additional classes that are not defined in the ISO classes.
Immersion Methods
Click on each image for more details.
Objectives can be divided by what medium they are designed to image through. Dry objectives are used in air; whereas dipping and immersion objectives are designed to operate with a fluid between the objective and the front element of the sample.
| Glossary of Terms | |
|---|---|
| Back Focal Length and Infinity Correction | The back focal length defines the location of the intermediate image plane. Most modern objectives will have this plane at infinity, known as infinity correction, and will signify this with an infinity symbol (∞). Infinity-corrected objectives are designed to be used with a tube lens between the objective and eyepiece. Along with increasing intercompatibility between microscope systems, having this infinity-corrected space between the objective and tube lens allows for additional modules (like beamsplitters, filters, or parfocal length extenders) to be placed in the beam path. Note that older objectives and some specialty objectives may have been designed with finite back focal lengths. In their inception, finite back focal length objectives were meant to interface directly with the objective's eyepiece. |
| Entrance Pupil Diameter (EP) | The entrance pupil diameter (EP), sometimes referred to as the entrance aperture diameter, corresponds to the appropriate beam diameter one should use to allow the objective to function properly. EP = 2 × NA × Effective Focal Length |
| Field Number (FN) and Field of View (FOV) |
The field number corresponds to the diameter of the field of view in object space (in millimeters) multiplied by the objective's magnification. Field Number = Field of View Diameter × Magnification |
| Magnification (M) | The magnification (M) of an objective is the lens tube focal length (L) divided by the objective's effective focal length (F). Effective focal length is sometimes abbreviated EFL: M = L / EFL . The total magnification of the system is the magnification of the objective multiplied by the magnification of the eyepiece or camera tube. The specified magnification on the microscope objective housing is accurate as long as the objective is used with a compatible tube lens focal length. Objectives will have a colored ring around their body to signify their magnification. This is fairly consistent across manufacturers; see the Parts of a Microscope Objective section for more details. |
| Numerical Aperture (NA) | Numerical aperture, a measure of the acceptance angle of an objective, is a dimensionless quantity. It is commonly expressed as: NA = ni × sinθa where θa is the maximum 1/2 acceptance angle of the objective, and ni is the index of refraction of the immersion medium. This medium is typically air, but may also be water, oil, or other substances. |
| Working Distance (WD) |
The working distance, often abbreviated WD, is the distance between the front element of the objective and the top of the specimen (in the case of objectives that are intended to be used without a cover glass) or top of the cover glass, depending on the design of the objective. The cover glass thickness specification engraved on the objective designates whether a cover glass should be used. |
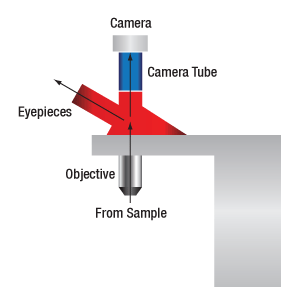
When viewing an image with a camera, the system magnification is the product of the objective and camera tube magnifications. When viewing an image with trinoculars, the system magnification is the product of the objective and eyepiece magnifications.
| Manufacturer | Tube Lens Focal Length |
|---|---|
| Leica | f = 200 mm |
| Mitutoyo | f = 200 mm |
| Nikon | f = 200 mm |
| Olympus | f = 180 mm |
| Thorlabs | f = 200 mm |
| Zeiss | f = 165 mm |
Magnification and Sample Area Calculations
Magnification
The magnification of a system is the multiplicative product of the magnification of each optical element in the system. Optical elements that produce magnification include objectives, camera tubes, and trinocular eyepieces, as shown in the drawing to the right. It is important to note that the magnification quoted in these products' specifications is usually only valid when all optical elements are made by the same manufacturer. If this is not the case, then the magnification of the system can still be calculated, but an effective objective magnification should be calculated first, as described below.
To adapt the examples shown here to your own microscope, please use our Magnification and FOV Calculator, which is available for download by clicking on the red button above. Note the calculator is an Excel spreadsheet that uses macros. In order to use the calculator, macros must be enabled. To enable macros, click the "Enable Content" button in the yellow message bar upon opening the file.
Example 1: Camera Magnification
When imaging a sample with a camera, the image is magnified by the objective and the camera tube. If using a 20X Nikon objective and a 0.75X Nikon camera tube, then the image at the camera has 20X × 0.75X = 15X magnification.
Example 2: Trinocular Magnification
When imaging a sample through trinoculars, the image is magnified by the objective and the eyepieces in the trinoculars. If using a 20X Nikon objective and Nikon trinoculars with 10X eyepieces, then the image at the eyepieces has 20X × 10X = 200X magnification. Note that the image at the eyepieces does not pass through the camera tube, as shown by the drawing to the right.
Using an Objective with a Microscope from a Different Manufacturer
Magnification is not a fundamental value: it is a derived value, calculated by assuming a specific tube lens focal length. Each microscope manufacturer has adopted a different focal length for their tube lens, as shown by the table to the right. Hence, when combining optical elements from different manufacturers, it is necessary to calculate an effective magnification for the objective, which is then used to calculate the magnification of the system.
The effective magnification of an objective is given by Equation 1:
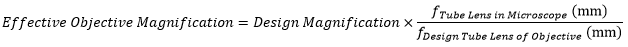 |
(Eq. 1) |
Here, the Design Magnification is the magnification printed on the objective, fTube Lens in Microscope is the focal length of the tube lens in the microscope you are using, and fDesign Tube Lens of Objective is the tube lens focal length that the objective manufacturer used to calculate the Design Magnification. These focal lengths are given by the table to the right.
Note that Leica, Mitutoyo, Nikon, and Thorlabs use the same tube lens focal length; if combining elements from any of these manufacturers, no conversion is needed. Once the effective objective magnification is calculated, the magnification of the system can be calculated as before.
Example 3: Trinocular Magnification (Different Manufacturers)
When imaging a sample through trinoculars, the image is magnified by the objective and the eyepieces in the trinoculars. This example will use a 20X Olympus objective and Nikon trinoculars with 10X eyepieces.
Following Equation 1 and the table to the right, we calculate the effective magnification of an Olympus objective in a Nikon microscope:
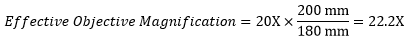 |
The effective magnification of the Olympus objective is 22.2X and the trinoculars have 10X eyepieces, so the image at the eyepieces has 22.2X × 10X = 222X magnification.
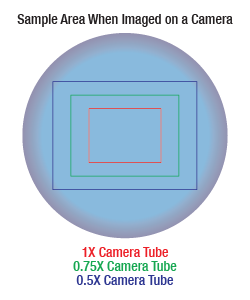
Sample Area When Imaged on a Camera
When imaging a sample with a camera, the dimensions of the sample area are determined by the dimensions of the camera sensor and the system magnification, as shown by Equation 2.
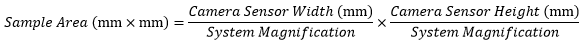 |
(Eq. 2) |
The camera sensor dimensions can be obtained from the manufacturer, while the system magnification is the multiplicative product of the objective magnification and the camera tube magnification (see Example 1). If needed, the objective magnification can be adjusted as shown in Example 3.
As the magnification increases, the resolution improves, but the field of view also decreases. The dependence of the field of view on magnification is shown in the schematic to the right.
Example 4: Sample Area
The dimensions of the camera sensor in Thorlabs' previous-generation 1501M-USB Scientific Camera are 8.98 mm × 6.71 mm. If this camera is used with the Nikon objective and trinoculars from Example 1, which have a system magnification of 15X, then the image area is:
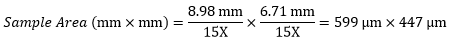 |
Sample Area Examples
The images of a mouse kidney below were all acquired using the same objective and the same camera. However, the camera tubes used were different. Read from left to right, they demonstrate that decreasing the camera tube magnification enlarges the field of view at the expense of the size of the details in the image.
Resolution Tutorial
An important parameter in many imaging applications is the resolution of the objective. This tutorial describes the different conventions used to define an objective's resolution. Thorlabs provides the theoretical Rayleigh resolution for all of the imaging objectives offered on our site; the other conventions are presented for informational purposes.
Resolution
The resolution of an objective refers to its ability to distinguish closely-spaced features of an object. This is often theoretically quantified by considering an object that consists of two point sources and asking at what minimum separation can these two point sources be resolved. When a point source is imaged, rather than appearing as a singular bright point, it will appear as a broadened intensity profile due to the effects of diffraction. This profile, known as an Airy disk, consists of an intense central peak with surrounding rings of much lesser intensity. The image produced by two point sources in proximity to one another will therefore consist of two overlapping Airy disk profiles, and the resolution of the objective is therefore determined by the minimum spacing at which the two profiles can be uniquely identified. There is no fundamental criterion for establishing what exactly it means for the two profiles to be resolved and, as such, there are a few criteria that are observed in practice. In microscopic imaging applications, the two most commonly used criteria are the Rayleigh and Abbe criteria. A third criterion, more common in astronomical applications, is the Sparrow criterion.
Rayleigh Criterion
The Rayleigh criterion states that two overlapping Airy disk profiles are resolved when the first intensity minimum of one profile coincides with the intensity maximum of the other profile [1]. It can be shown that the first intensity minimum occurs at a radius of 1.22λf/D from the central maximum, where λ is the wavelength of the light, f is the focal length of the objective, and D is the entrance pupil diameter. Thus, in terms of the numerical aperture (NA = 0.5*D/f), the Rayleigh resolution is:
rR = 0.61λ/NA
An idealized image of two Airy disks separated by a distance equal to the Rayleigh resolution is shown in the figure to the left below; the illumination source has been assumed to be incoherent. A corresponding horizontal line cut across the intensity maxima is plotted to the right. The vertical dashed lines in the intensity profile show that the maximum of each individual Airy disk overlaps with the neighboring minimum. Between the two maxima, there is a local minimum which appears in the image as a gray region between the two white peaks.
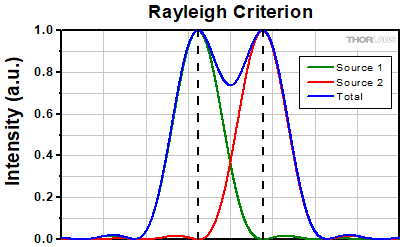 Click to Enlarge
Click to EnlargeLeft: Two point sources are considered resolved when separated by the Rayleigh resolution. The gray region between the two white peaks is clearly visible.
Above: The vertical dashed lines show how the maximum of each intensity profile overlaps with the first minimum of the other.

Thorlabs provides the theoretical Rayleigh resolution for all of the imaging objectives offered on our site in their individual product presentations.
Abbe Criterion
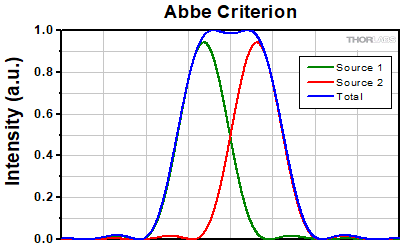
The Abbe theory describes image formation as a double process of diffraction [2]. Within this framework, if two features separated by a distance d are to be resolved, at a minimum both the zeroth and first orders of diffraction must be able to pass through the objective's aperture. Since the first order of diffraction appears at the angle: sin(θ1) = λ/d, the minimum object separation, or equivalently the resolution of the objective, is given by d = λ/n*sin(α), where α is the angular semi-aperture of the objective and a factor of n has been inserted to account for the refractive index of the imaging medium. This result overestimates the actual limit by a factor of 2 because both first orders of diffraction are assumed to be accepted by the objective, when in fact only one of the first orders must pass through along with the zeroth order. Dividing the above result by a factor of 2 and using the definition of the numerical aperture (NA = n*sin(α)) gives the famous Abbe resolution limit:
rA = 0.5λ/NA
In the image below, two Airy disks are shown separated by the Abbe resolution limit. Compared to the Rayleigh limit, the decrease in intensity at the origin is much harder to discern. The horizontal line cut to the right shows that the intensity decreases by only ≈2%.
 Click to Enlarge
Click to EnlargeLeft: Two point sources separated by the Abbe resolution limit. Though observable, the contrast between the maxima and central minimum is much weaker compared to the Rayleigh limit.
Above: The line cut shows the small intensity dip between the two maxima.

Sparrow Criterion
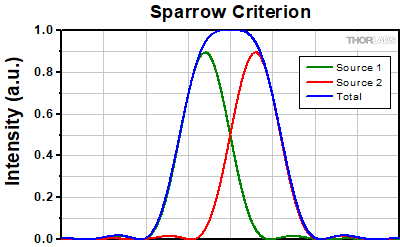
For point source separations corresponding to the Rayleigh and Abbe resolution criteria, the combined intensity profile has a local minimum located at the origin between the two maxima. In a sense, this feature is what allows the two point sources to be resolved. That is to say, if the sources' separation is further decreased beyond the Abbe resolution limit, the two individual maxima will merge into one central maximum and resolving the two individual contributions will no longer be possible. The Sparrow criterion posits that the resolution limit is reached when the crossover from a central minimum to a central maximum occurs.
At the Sparrow resolution limit, the center of the combined intensity profile is flat, which implies that the derivative with respect to position is zero at the origin. However, this first derivative at the origin is always zero, given that it is either a local minimum or maximum of the combined intensity profile (strictly speaking, this is only the case if the sources have equal intensities). Consider then, that because the Sparrow resolution limit occurs when the origin's intensity changes from a local minimum to a maximum, that the second derivative must be changing sign from positive to negative. The Sparrow criterion is thus a condition that is imposed upon the second derivative, namely that the resolution limit occurs when the second derivative is zero [3]. Applying this condition to the combined intensity profile of two Airy disks leads to the Sparrow resolution:
rS = 0.47λ/NA
The image to the left below shows two Airy disks separated by the Sparrow resolution limit. As described above, the intensity is constant in the region between the two peaks and there is no intensity dip at the origin. In the line cut to the right, the constant intensity near the origin is confirmed.
 Click to Enlarge
Click to EnlargeLeft: Two Airy disk profiles separated by the Sparrow resolution limit. Note that, unlike the Rayleigh or Abbe limits, there is no decrease in intensity at the origin.
Above: At the Sparrow resolution limit, the combined intensity is a constant near the origin. The scale here has been normalized to 1.

References
[1] Eugene Hecht, "Optics," 4th Ed., Addison-Wesley (2002)
[2] S.G. Lipson, H. Lipson, and D.S. Tannhauser, "Optical Physics," 3rd Ed., Cambridge University Press (1995)
[3] C.M. Sparrow, "On Spectroscopic Resolving Power," Astrophys. J. 44, 76-87 (1916)
| Posted Comments: | |
li yancheng
(posted 2023-05-31 01:37:40.667) how many dispersion(GVD)(fs^2/mm) Will this product apply at wavelength:900nm、1200nm?
N40XLWD-NIR - 40X Nikon CFI APO LWD NIR Objective, 1.15 NA, 0.59 - 0.61 mm WD cdolbashian
(posted 2023-06-01 03:53:14.0) Thank you for reaching out to us with this inquiry. While we at Thorlabs would love to provide you with such an answer, these are Nikon objectives, and as such, we do not have access to their test data. ZL QU
(posted 2023-03-22 16:34:02.103) Can this objective lens be mounted on an inverted microscope? If so, how to prevent water from spilling when the objective is upside down ksosnowski
(posted 2023-04-03 01:36:54.0) Hello, thanks for reaching out to Thorlabs. These Immersion Objectives are intended for upright use and in inverted applications there is no mechanism to catch spills. Depending on the exact setup it may be possible to contain a small bead of liquid between the objective and sample with the media surface tension however we have not tested this type of application. I've reached out directly to discuss this setup further. William Frost
(posted 2022-05-13 18:09:06.233) We would like to try out the N16XLWD-PF Nikon objective lens as a way to decide whether we will purchase it. Is that possible? Feel free to connect me with a sales person that could help me with this. jdelia
(posted 2022-05-20 11:49:00.0) Thank you for contacting Thorlabs. I have contacted you directly regarding the possibility of loaning out these objectives. Robert Campbell
(posted 2021-11-10 12:40:07.423) Hello,
I'm incorporating the N16XLWD-PF and I need to know its weight (not the shipping weight, which I've found elsewhere). It is being used on a dynamically tuned focus stage & it is replacing an existing objective, so I need to match the overall mass of the objective and mounting bracket. I will need to either add or remove weight depending on the weight of the N16XLWD-PF.
Thanks,
Rob Campbell YLohia
(posted 2021-11-12 04:06:52.0) Hello Rob, thank you for contacting Thorlabs. The approximate weight of this Nikon objective is listed in the engineering drawing (AutoCAD pdf) as 0.13 kg. Gerd Wiebusch
(posted 2020-02-19 14:54:40.183) Dir Sirs,
is it possible to test (borrow) this new objective before buying?
Best regards
Gerd Wiebusch llamb
(posted 2020-02-20 04:07:44.0) Hello Gerd, thank you for your interest in Thorlabs products. Unfortunately we will not be able to offer loan/test units on our objective lenses. user
(posted 2019-08-08 12:55:18.337) The diameter of the front glass of this objective is 6 mm and not 6.4 mm mentioned in your Auto CAD PDF file. I appended the link from the manufacturer.
https://www.microscope.healthcare.nikon.com/images/diagrams/Optics/CFI75-Water-Dipping-Series/cfi75_lwd_16x_w.svg llamb
(posted 2019-08-08 03:17:25.0) Thank you for bringing this to our attention. We will update our online drawings accordingly. |

Click to Enlarge
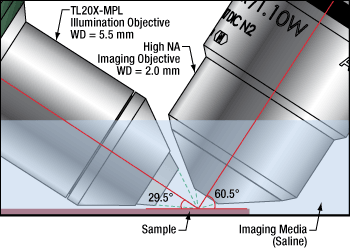
The TL20X-MPL objective in a light sheet microscopy set up. The steep housing angle and long working distance (WD) allow for positioning in tight imaging areas.
- Designed as an Excitation Objective for Lattice Light Sheet Microscopy
- Infinity-Corrected Apochromatic Design
- 20X Magnification When Used With a 200 mm Tube Lens
- Water-Tight Seal for Water Dipping
- M25 x 0.75 Threading
Thorlabs' TL20X-MPL Water Dipping Objective is designed primarily as an excitation objective especially suited for lattice light sheet multiphoton microscopy and other applications with tightly confined space near the focus region. With a long working distance, narrow diameter, and steep approach angle at the distal tip, this objective provides the minimized footprint needed in many physiology applications where other optics or tools are manipulated near the sample.
The example diagram to the right illustrates how the TL20X-MPL objective can be used for excitation in Bessel beam lattice light sheet multiphoton microscopy. The long 5.5 mm working distance provides the space needed when orienting the TL20X-MPL objective next to an imaging objective and is beneficial for producing the large excitation sheet required for lattice light sheet microscopy.
The TL20X-MPL objective provides 20X magnification and has the longest working distance of our available water dipping or immersion objectives. The apochromatic design provides excellent color correction from 400 nm to 900 nm. This objective provides diffraction limited performance across the defined wavelength range with slight refocus on the order of 1 µm required through the visible spectrum; click the blue info icon (![]() ) in the table below to view performance data for this lens.
) in the table below to view performance data for this lens.
The lenses in this objective are sealed with a specialized two-part epoxy that is safe for use with biological samples. The TL20X-MPL objective features M25 x 0.75 threading and is compatible with our
DIY Cerna® Systems. Thorlabs offers the M32M25S thread adapter for converting to M32 x 0.75 threads.

| Protective Accessories | |
|---|---|
| Objective | Objective Case |
| N25X-APO-MP | Lid: OC2M32 Canister: OC24 |
| N25X-APO-MP1300 | |
| N40XLWD-NIR | Lid: OC2M25 Canister: OC24 |
| N40X-NIR | |
| N40X-NIR | |
- Ideal for Multiphoton Imaging and Life Science Applications
- Infinity-Corrected Apochromatic Design
- Magnifications Specified When Used With a 200 mm Tube Lens
- M32 x 0.75 or M25 x 0.75 Threading
These Nikon Apochromatic Water Dipping Objectives provide 20X, 40X, or 60X magnification. Their designation as apochromatic indicates that these objectives provide excellent color correction throughout their defined wavelength ranges including at near-infrared (NIR) wavelengths. These objectives are suitable for fluorescence microscopy, brightfield microscopy, and DIC microscopy including NIR DIC.
The N25X-APO-MP and N25X-APO-MP1300 objectives feature a rotating coverslip correction collar to correct aberration for coverslips that are 0 to 0.17 mm thick, with 0 mm indicating that these can be used as water dipping objectives without a coverslip. The N40XLWD-NIR objective features a correction collar for coverslips that are 0.15 - 0.91 mm thick. All three of these objectives also feature spring-loaded retractable housing designs to protect the optics and sample from collision damage.
To use these objectives with a different thread standard, please see our microscope objective thread adapters.
| Item # | Wavelength Range | M | WD | EFL | NA | EPa | PFL | Coverslip Correctionb |
Immersion Method | Objective Threading |
|---|---|---|---|---|---|---|---|---|---|---|
| N25X-APO-MP | 380 - 1050 nm | 25X | 2.0 mm | 8.0 mm | 1.10 | 17.6 mm | 75 mm | 0 - 0.17 mm | Water Dipping or Water Immersion (Coverslip) |
M32 x 0.75 4.7 mm Depth |
| N25X-APO-MP1300 | 420 - 1400 nm | |||||||||
| N40XLWD-NIR | 360 - 1100 nm | 40X | 0.59 - 0.61 mm | 5.0 mm | 1.15 | 11.5 mm | 60 mm | 0.15 - 0.19 mm | Water Immersion (Coverslip) | M25 x 0.75 5.1 mm Depth |
| N40X-NIR | 380 - 1100 nm | 3.5 mm | 5.0 mm | 0.80 | 8.0 mm | N/A | Water Dipping | |||
| N60X-NIR | 60X | 2.8 mm | 3.3 mm | 1.0 | 6.7 mm |

| Protective Accessories | |
|---|---|
| Objective | Objective Case |
| N10XW-PF | Lid: OC2M25 Canister: OC24 |
| N16XLWD-PF | Lid: OC2M32 Canister: OC24 |
- Ideal for Multiphoton Imaging and Life Science Applications
- Infinity-Corrected Plan Fluorite Design
- Magnifications Specified When Used With a 200 mm Tube Lens
- M32 x 0.75 or M25 x 0.75 Threading
These Nikon Plan Fluorite Water Dipping Objectives provide 10X or 16X magnification. Their designation as plan fluorite indicates that these objectives produce a flat plane of focus and are corrected for spherical and chromatic aberrations at multiple wavelengths. Both of these objectives are excellent for fluorescence microscopy, brightfield microscopy, and DIC microscopy, while the N10XW-PF objective is corrected for wavelengths down to 360 nm, making it suitable for UV fluorescence.
To use these objectives with a different thread standard, please see our microscope objective thread adapters.
| Item # | Wavelength Range | M | WD | EFL | NA | EPa | PFL | Coverslip Correction |
Immersion Method | Objective Threading |
|---|---|---|---|---|---|---|---|---|---|---|
| N10XW-PF | 360 - 1500 nm | 10X | 3.5 mm | 20 mm | 0.30 | 12.0 mm | 60 mm | N/A | Water Dipping | M25 x 0.75 5.1 mm Depth |
| N16XLWD-PF | 380 - 1100 nm | 16X | 3.0 mm | 12.5 mm | 0.80 | 20.0 mm | 75 mm | M32 x 0.75 5.0 mm Depth |

- Ideal for Fluorescence Microscopy and Life Science Applications
- Infinity-Corrected Plan Fluorite Design
- 20X Magnification When Used With a 180 mm Tube Lens
- M25 x 0.75 Threading
This Olympus Plan Fluorite Water Dipping Objective provides 20X magnification and features axial color correction for 400 to 900 nm. The designation as plan fluorite indicates that this objective produces a flat plane of focus and is corrected for spherical and chromatic aberrations at multiple wavelengths. This objective is excellent for fluorescence microscopy, brightfield microscopy, and DIC microscopy.
The N20X-PFH objective features M25 x 0.75 threading; to convert to M32 x 0.75 threads, we offer the M32M25S thread adapter. This objective has a large entrance pupil diameter (EP) and is designed for a tube lens with focal length 180 mm.
| Item # | Wavelength Range | M | WD | EFL | NA | EPa | PFL | Coverslip Correction |
Immersion Method | Objective Threading |
|---|---|---|---|---|---|---|---|---|---|---|
| N20X-PFH | 400 - 900 nm | 20X | 2.00 mm | 9.0 mm | 1.00 | 18 mm | 75 mm | N/A | Water Dipping | M25 x 0.75 5.8 mm Depth |
 Products Home
Products Home

















 Zoom
Zoom


 Physiology Objectives, Water Dipping & Immersion
Physiology Objectives, Water Dipping & Immersion