Imaging/Focusing Microscope Objectives, Oil Immersion

- Infinity-Corrected Microscope Objectives for UV, Visible, and NIR
- Designed for Oil Immersion Medium Applications
- Magnifications Ranging from 40X to 100X
RMS100X-O
100X Plan Achromat
RMS100X-PFOD
100X Plan Fluorite
N100X-PFO
100X Plan Fluorite
MOIL-30
Immersion Oil

Please Wait
| Objective Lens Selection Guide |
|---|
| Objectives |
| Super Apochromatic Microscope Objectives Microscopy Objectives, Dry Microscopy Objectives, Oil Immersion Physiology Objectives, Water Dipping or Immersion Phase Contrast Objectives Long Working Distance Objectives Reflective Microscopy Objectives UV Focusing Objectives VIS and NIR Focusing Objectives |
| Scan Lenses and Tube Lenses |
| Scan Lenses F-Theta Scan Lenses Infinity-Corrected Tube Lenses |

Did You Know?
Multiple optical elements, including the microscope objective, tube lens, and eyepieces, together define the magnification of a system. See the Magnification & FOV tab to learn more.
Click for Details
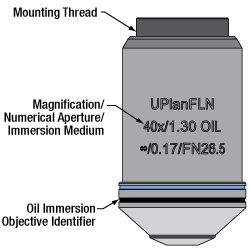
Example of an Oil Immersion Objective Design
(See Objective Tutorial Tab for More Information About Microscope Objective Types)
Thorlabs offers oil immersion objective designs from Olympus and Nikon. The majority of the objectives are plan fluorite objectives, while one (RMS100X-O) is a plan achromat design. For details about the differences between these types of objectives, please see the Objective Tutorial tab above.
These microscope objectives should be used in applications like traditional and multiphoton microscopy and confocal imaging and are suitable for a variety of imaging modalities, including epi-illumination, oblique illumination, brightfield, and DIC applications. These infinity-corrected objectives have optical elements with an ultra-wide broadband AR coating, designed for use with either 180 mm or 200 mm focal length tube lenses.
The Olympus objectives on this page have RMS (0.800"-36) threading, and the Nikon objective has M25 x 0.75 threading. To use these objectives with a different thread standard, please see our microscope objective thread adapters. When choosing a microscope objective, it is important to keep in mind that objectives are often designed to integrate with a particular manufacturer's microscopes and are not necessarily interchangeable due to tube length differences and variations in thread pitch or diameter. Please note that the performance of each objective may vary from the engraved specifications when integrated with components and systems from different manufacturers. See the Magnification and FOV tab for more information.
All objectives featured on this page are compatible with our microscope nosepiece modules for DIY Cerna® systems, which accept RMS, M25 x 0.75, or M32 x 0.75 objective threading.
| Oil-Immersion Objectives | ||||||
|---|---|---|---|---|---|---|
| Item # | RMS40X-PFO | RMS60X-PFOD | RMS100X-PFOa | RMS100X-PFOD | RMS100X-O | N100X-PFOa |
| Manufacturer | Olympus | Nikon | ||||
| Manufacturer Part # | 1-U2B530 | 1-U2B532 | 1-U2B5352 | 1-U2B5362 | 1-U2B235 | MRH01902 |
| Magnification | 40X | 60X | 100X | 100X | 100X | 100X |
| Numerical Aperture (NA) | 1.3 | 1.25 - 0.65 | 1.3 | 1.3 - 0.55 | 1.25 | 1.3 |
| Effective Focal Length (EFL) | 4.5 mm | 3 mm | 1.8 mm | 1.8 mm | 1.8 mm | 2.0 mm |
| Entrance Pupil Diameterb | 11.7 mm | 7.5 - 3.9 mm | 4.7 mm | 4.7 - 2.0 mm | 4.5 mm | 5.2 mm |
| Field Number | 26.5 | 26.5 | 26.5 | 26.5 | 22 | N/A |
| Resolutionc | 0.3 µm | 0.3 µmd | 0.3 µm | 0.3 µmd | 0.3 µm | 0.3 µm |
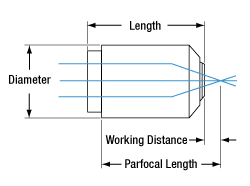
| Working Distance (WD)e | 0.2 mm | 0.12 mm | 0.2 mm | 0.2 mm | 0.15 mm | 0.16 mm |
| Parfocal Lengthe | 45.06 mm | 60 mm | ||||
| Compatible Tube Lens Focal Length | 180 mm | 200 mm | ||||
| Coverslip Correction | 0.17 mm | - | 0.17 mm | |||
| Diametere | 28 mm | 28 mm | 26 mm | 28 mm | 24 mm | 30 mm |
| Lengthe | 49.4 mm | 49.5 mm | 49.2 mm | 49.3 mm | 49.2 mm | 64.8 mm |
| Design Wavelength | Visible and NIR | Visible | Visible | |||
| Threading | RMS | M25 x 0.75 | ||||
| Thread Depth | 4.7 mm | 4.7 mm | 4.5 mm | 4.5 mm | 4.5 mm | 5.1 mm |
Dimensional Drawing
| Chromatic Aberration Correction per ISO Standard 19012-2 | ||
|---|---|---|
| Objective Class | Common Abbreviations | Axial Focal Shift Tolerancesa |
| Achromat | ACH, ACHRO, ACHROMAT | |δC' - δF'| ≤ 2 x δob |
| Semiapochromat (or Fluorite) |
SEMIAPO, FL, FLU | |δC' - δF'| ≤ 2 x δob |δF' - δe| ≤ 2.5 x δob |δC' - δe| ≤ 2.5 x δob |
| Apochromat | APO | |δC' - δF'| ≤ 2 x δob |δF' - δe| ≤ δob |δC' - δe| ≤ δob |
| Super Apochromat | SAPO | See Footnote b |
| Improved Visible Apochromat | VIS+ | See Footnotes b and c |
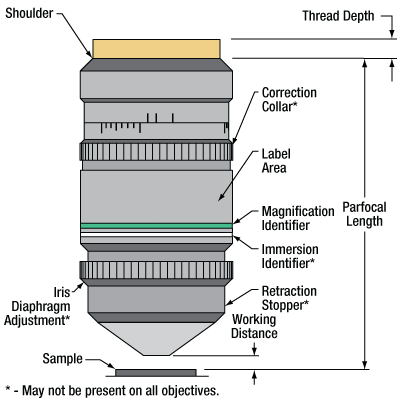
Parts of a Microscope Objective
Click on each label for more details.
This microscope objective serves only as an example. The features noted above with an asterisk may not be present on all objectives; they may be added, relocated, or removed from objectives based on the part's needs and intended application space.
Objective Tutorial
This tutorial describes features and markings of objectives and what they tell users about an objective's performance.
Objective Class and Aberration Correction
Objectives are commonly divided by their class. An objective's class creates a shorthand for users to know how the objective is corrected for imaging aberrations. There are two types of aberration corrections that are specified by objective class: field curvature and chromatic aberration.
Field curvature (or Petzval curvature) describes the case where an objective's plane of focus is a curved spherical surface. This aberration makes widefield imaging or laser scanning difficult, as the corners of an image will fall out of focus when focusing on the center. If an objective's class begins with "Plan", it will be corrected to have a flat plane of focus.
Images can also exhibit chromatic aberrations, where colors originating from one point are not focused to a single point. To strike a balance between an objective's performance and the complexity of its design, some objectives are corrected for these aberrations at a finite number of target wavelengths.
Five objective classes are shown in the table to the right; only three common objective classes are defined under the International Organization for Standards ISO 19012-2: Microscopes -- Designation of Microscope Objectives -- Chromatic Correction. Due to the need for better performance, we have added two additional classes that are not defined in the ISO classes.
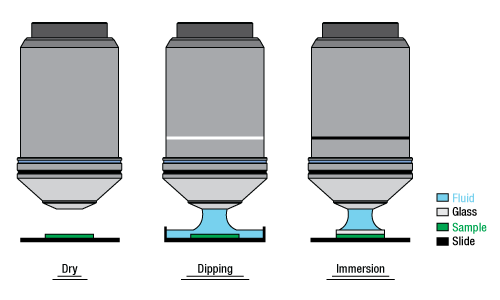
Immersion Methods
Click on each image for more details.
Objectives can be divided by what medium they are designed to image through. Dry objectives are used in air; whereas dipping and immersion objectives are designed to operate with a fluid between the objective and the front element of the sample.
| Glossary of Terms | |
|---|---|
| Back Focal Length and Infinity Correction | The back focal length defines the location of the intermediate image plane. Most modern objectives will have this plane at infinity, known as infinity correction, and will signify this with an infinity symbol (∞). Infinity-corrected objectives are designed to be used with a tube lens between the objective and eyepiece. Along with increasing intercompatibility between microscope systems, having this infinity-corrected space between the objective and tube lens allows for additional modules (like beamsplitters, filters, or parfocal length extenders) to be placed in the beam path. Note that older objectives and some specialty objectives may have been designed with finite back focal lengths. In their inception, finite back focal length objectives were meant to interface directly with the objective's eyepiece. |
| Entrance Pupil Diameter (EP) | The entrance pupil diameter (EP), sometimes referred to as the entrance aperture diameter, corresponds to the appropriate beam diameter one should use to allow the objective to function properly. EP = 2 × NA × Effective Focal Length |
| Field Number (FN) and Field of View (FOV) |
The field number corresponds to the diameter of the field of view in object space (in millimeters) multiplied by the objective's magnification. Field Number = Field of View Diameter × Magnification |
| Magnification (M) | The magnification (M) of an objective is the lens tube focal length (L) divided by the objective's effective focal length (F). Effective focal length is sometimes abbreviated EFL: M = L / EFL . The total magnification of the system is the magnification of the objective multiplied by the magnification of the eyepiece or camera tube. The specified magnification on the microscope objective housing is accurate as long as the objective is used with a compatible tube lens focal length. Objectives will have a colored ring around their body to signify their magnification. This is fairly consistent across manufacturers; see the Parts of a Microscope Objective section for more details. |
| Numerical Aperture (NA) | Numerical aperture, a measure of the acceptance angle of an objective, is a dimensionless quantity. It is commonly expressed as: NA = ni × sinθa where θa is the maximum 1/2 acceptance angle of the objective, and ni is the index of refraction of the immersion medium. This medium is typically air, but may also be water, oil, or other substances. |
| Working Distance (WD) |
The working distance, often abbreviated WD, is the distance between the front element of the objective and the top of the specimen (in the case of objectives that are intended to be used without a cover glass) or top of the cover glass, depending on the design of the objective. The cover glass thickness specification engraved on the objective designates whether a cover glass should be used. |
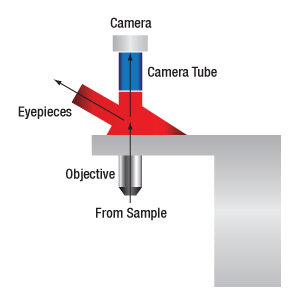
When viewing an image with a camera, the system magnification is the product of the objective and camera tube magnifications. When viewing an image with trinoculars, the system magnification is the product of the objective and eyepiece magnifications.
| Manufacturer | Tube Lens Focal Length |
|---|---|
| Leica | f = 200 mm |
| Mitutoyo | f = 200 mm |
| Nikon | f = 200 mm |
| Olympus | f = 180 mm |
| Thorlabs | f = 200 mm |
| Zeiss | f = 165 mm |
Magnification and Sample Area Calculations
Magnification
The magnification of a system is the multiplicative product of the magnification of each optical element in the system. Optical elements that produce magnification include objectives, camera tubes, and trinocular eyepieces, as shown in the drawing to the right. It is important to note that the magnification quoted in these products' specifications is usually only valid when all optical elements are made by the same manufacturer. If this is not the case, then the magnification of the system can still be calculated, but an effective objective magnification should be calculated first, as described below.
To adapt the examples shown here to your own microscope, please use our Magnification and FOV Calculator, which is available for download by clicking on the red button above. Note the calculator is an Excel spreadsheet that uses macros. In order to use the calculator, macros must be enabled. To enable macros, click the "Enable Content" button in the yellow message bar upon opening the file.
Example 1: Camera Magnification
When imaging a sample with a camera, the image is magnified by the objective and the camera tube. If using a 20X Nikon objective and a 0.75X Nikon camera tube, then the image at the camera has 20X × 0.75X = 15X magnification.
Example 2: Trinocular Magnification
When imaging a sample through trinoculars, the image is magnified by the objective and the eyepieces in the trinoculars. If using a 20X Nikon objective and Nikon trinoculars with 10X eyepieces, then the image at the eyepieces has 20X × 10X = 200X magnification. Note that the image at the eyepieces does not pass through the camera tube, as shown by the drawing to the right.
Using an Objective with a Microscope from a Different Manufacturer
Magnification is not a fundamental value: it is a derived value, calculated by assuming a specific tube lens focal length. Each microscope manufacturer has adopted a different focal length for their tube lens, as shown by the table to the right. Hence, when combining optical elements from different manufacturers, it is necessary to calculate an effective magnification for the objective, which is then used to calculate the magnification of the system.
The effective magnification of an objective is given by Equation 1:
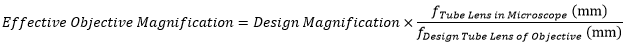 |
(Eq. 1) |
Here, the Design Magnification is the magnification printed on the objective, fTube Lens in Microscope is the focal length of the tube lens in the microscope you are using, and fDesign Tube Lens of Objective is the tube lens focal length that the objective manufacturer used to calculate the Design Magnification. These focal lengths are given by the table to the right.
Note that Leica, Mitutoyo, Nikon, and Thorlabs use the same tube lens focal length; if combining elements from any of these manufacturers, no conversion is needed. Once the effective objective magnification is calculated, the magnification of the system can be calculated as before.
Example 3: Trinocular Magnification (Different Manufacturers)
When imaging a sample through trinoculars, the image is magnified by the objective and the eyepieces in the trinoculars. This example will use a 20X Olympus objective and Nikon trinoculars with 10X eyepieces.
Following Equation 1 and the table to the right, we calculate the effective magnification of an Olympus objective in a Nikon microscope:
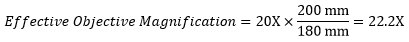 |
The effective magnification of the Olympus objective is 22.2X and the trinoculars have 10X eyepieces, so the image at the eyepieces has 22.2X × 10X = 222X magnification.
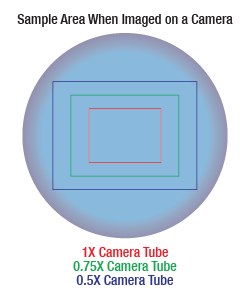
Sample Area When Imaged on a Camera
When imaging a sample with a camera, the dimensions of the sample area are determined by the dimensions of the camera sensor and the system magnification, as shown by Equation 2.
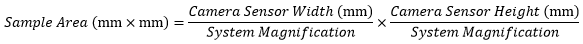 |
(Eq. 2) |
The camera sensor dimensions can be obtained from the manufacturer, while the system magnification is the multiplicative product of the objective magnification and the camera tube magnification (see Example 1). If needed, the objective magnification can be adjusted as shown in Example 3.
As the magnification increases, the resolution improves, but the field of view also decreases. The dependence of the field of view on magnification is shown in the schematic to the right.
Example 4: Sample Area
The dimensions of the camera sensor in Thorlabs' previous-generation 1501M-USB Scientific Camera are 8.98 mm × 6.71 mm. If this camera is used with the Nikon objective and trinoculars from Example 1, which have a system magnification of 15X, then the image area is:
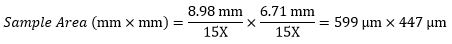 |
Sample Area Examples
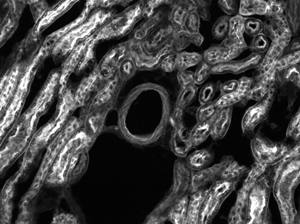
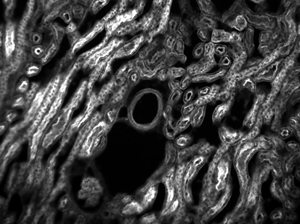
The images of a mouse kidney below were all acquired using the same objective and the same camera. However, the camera tubes used were different. Read from left to right, they demonstrate that decreasing the camera tube magnification enlarges the field of view at the expense of the size of the details in the image.
Resolution Tutorial
An important parameter in many imaging applications is the resolution of the objective. This tutorial describes the different conventions used to define an objective's resolution. Thorlabs provides the theoretical Rayleigh resolution for all of the imaging objectives offered on our site; the other conventions are presented for informational purposes.
Resolution
The resolution of an objective refers to its ability to distinguish closely-spaced features of an object. This is often theoretically quantified by considering an object that consists of two point sources and asking at what minimum separation can these two point sources be resolved. When a point source is imaged, rather than appearing as a singular bright point, it will appear as a broadened intensity profile due to the effects of diffraction. This profile, known as an Airy disk, consists of an intense central peak with surrounding rings of much lesser intensity. The image produced by two point sources in proximity to one another will therefore consist of two overlapping Airy disk profiles, and the resolution of the objective is therefore determined by the minimum spacing at which the two profiles can be uniquely identified. There is no fundamental criterion for establishing what exactly it means for the two profiles to be resolved and, as such, there are a few criteria that are observed in practice. In microscopic imaging applications, the two most commonly used criteria are the Rayleigh and Abbe criteria. A third criterion, more common in astronomical applications, is the Sparrow criterion.
Rayleigh Criterion
The Rayleigh criterion states that two overlapping Airy disk profiles are resolved when the first intensity minimum of one profile coincides with the intensity maximum of the other profile [1]. It can be shown that the first intensity minimum occurs at a radius of 1.22λf/D from the central maximum, where λ is the wavelength of the light, f is the focal length of the objective, and D is the entrance pupil diameter. Thus, in terms of the numerical aperture (NA = 0.5*D/f), the Rayleigh resolution is:
rR = 0.61λ/NA
An idealized image of two Airy disks separated by a distance equal to the Rayleigh resolution is shown in the figure to the left below; the illumination source has been assumed to be incoherent. A corresponding horizontal line cut across the intensity maxima is plotted to the right. The vertical dashed lines in the intensity profile show that the maximum of each individual Airy disk overlaps with the neighboring minimum. Between the two maxima, there is a local minimum which appears in the image as a gray region between the two white peaks.
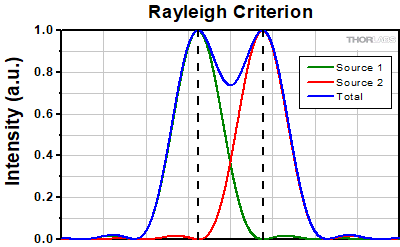 Click to Enlarge
Click to EnlargeLeft: Two point sources are considered resolved when separated by the Rayleigh resolution. The gray region between the two white peaks is clearly visible.
Above: The vertical dashed lines show how the maximum of each intensity profile overlaps with the first minimum of the other.

Thorlabs provides the theoretical Rayleigh resolution for all of the imaging objectives offered on our site in their individual product presentations.
Abbe Criterion
The Abbe theory describes image formation as a double process of diffraction [2]. Within this framework, if two features separated by a distance d are to be resolved, at a minimum both the zeroth and first orders of diffraction must be able to pass through the objective's aperture. Since the first order of diffraction appears at the angle: sin(θ1) = λ/d, the minimum object separation, or equivalently the resolution of the objective, is given by d = λ/n*sin(α), where α is the angular semi-aperture of the objective and a factor of n has been inserted to account for the refractive index of the imaging medium. This result overestimates the actual limit by a factor of 2 because both first orders of diffraction are assumed to be accepted by the objective, when in fact only one of the first orders must pass through along with the zeroth order. Dividing the above result by a factor of 2 and using the definition of the numerical aperture (NA = n*sin(α)) gives the famous Abbe resolution limit:
rA = 0.5λ/NA
In the image below, two Airy disks are shown separated by the Abbe resolution limit. Compared to the Rayleigh limit, the decrease in intensity at the origin is much harder to discern. The horizontal line cut to the right shows that the intensity decreases by only ≈2%.
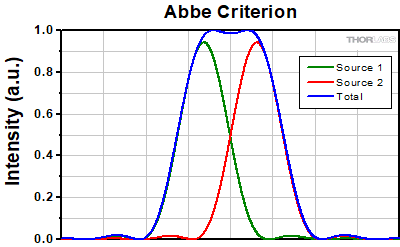 Click to Enlarge
Click to EnlargeLeft: Two point sources separated by the Abbe resolution limit. Though observable, the contrast between the maxima and central minimum is much weaker compared to the Rayleigh limit.
Above: The line cut shows the small intensity dip between the two maxima.

Sparrow Criterion
For point source separations corresponding to the Rayleigh and Abbe resolution criteria, the combined intensity profile has a local minimum located at the origin between the two maxima. In a sense, this feature is what allows the two point sources to be resolved. That is to say, if the sources' separation is further decreased beyond the Abbe resolution limit, the two individual maxima will merge into one central maximum and resolving the two individual contributions will no longer be possible. The Sparrow criterion posits that the resolution limit is reached when the crossover from a central minimum to a central maximum occurs.
At the Sparrow resolution limit, the center of the combined intensity profile is flat, which implies that the derivative with respect to position is zero at the origin. However, this first derivative at the origin is always zero, given that it is either a local minimum or maximum of the combined intensity profile (strictly speaking, this is only the case if the sources have equal intensities). Consider then, that because the Sparrow resolution limit occurs when the origin's intensity changes from a local minimum to a maximum, that the second derivative must be changing sign from positive to negative. The Sparrow criterion is thus a condition that is imposed upon the second derivative, namely that the resolution limit occurs when the second derivative is zero [3]. Applying this condition to the combined intensity profile of two Airy disks leads to the Sparrow resolution:
rS = 0.47λ/NA
The image to the left below shows two Airy disks separated by the Sparrow resolution limit. As described above, the intensity is constant in the region between the two peaks and there is no intensity dip at the origin. In the line cut to the right, the constant intensity near the origin is confirmed.
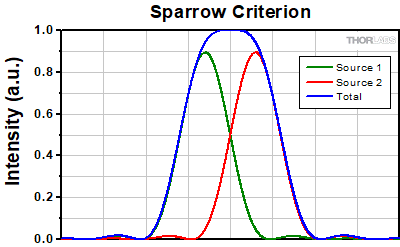 Click to Enlarge
Click to EnlargeLeft: Two Airy disk profiles separated by the Sparrow resolution limit. Note that, unlike the Rayleigh or Abbe limits, there is no decrease in intensity at the origin.
Above: At the Sparrow resolution limit, the combined intensity is a constant near the origin. The scale here has been normalized to 1.

References
[1] Eugene Hecht, "Optics," 4th Ed., Addison-Wesley (2002)
[2] S.G. Lipson, H. Lipson, and D.S. Tannhauser, "Optical Physics," 3rd Ed., Cambridge University Press (1995)
[3] C.M. Sparrow, "On Spectroscopic Resolving Power," Astrophys. J. 44, 76-87 (1916)
| Posted Comments: | |
Isael Herrera
(posted 2021-05-24 18:58:33.007) The note b) below the first table in section "specs" says:
"Entrance pupil diameter (EP) is defined at the back aperture of the objective and calculated as EP=2*NA*EFL. This formula is valid for oil objectives when the sample's refractive index is at least 1.50."
I think that the correct formula should be EP=2*NA*EFL/n, with n the index of refraction. Am I wrong? Otherwise, you are no considering the index of refraction (n =1.5) in the formula. YLohia
(posted 2021-05-27 03:04:31.0) Hello, thank you for your feedback. This equation assumes the index of refraction >= 1.5 in the calculation due to the definition of the NA spec (which includes the index of refraction). Please see the "Numerical Aperture (NA)" field under the "Glossary of Terms" table in the "Objective Tutorial" tab. Philip Binner
(posted 2020-10-30 13:27:24.633) 1.25-0.65 NA
I am confused by the notation of this ^. Does this mean the numerical aperture can take on any value between 0.65 and 1.25? YLohia
(posted 2020-10-30 02:08:32.0) Thank you for contacting Thorlabs. The -PFOD objectives have built-in irises that allow for the effective NA to be changed between the specified values (for example, between 0.65 and 1.25). |

- Oil Immersion Objectives for NIR and Visible Light
- Infinity-Corrected Plan Fluorite or Plan Achromat Designs
- Iris Diaphragm for Darkfield Microscopy on RMS60X-PFOD and RMS100X-PFOD
- RMS (0.800"-36) Threading
- Designed for a Tube Lens Focal Length of 180 mm
- 45.06 mm Parfocal Length
These objectives provide 40X, 60X, or 100X magnification, flat images across the entire visible spectrum, high numerical aperture values, and excellent resolution. The RMS40X-PFO, RMS50X-PFOD, RMS100X-PFO, and RMS100X-POFD are plan fluorite designs, while the RMS100X-O is a plan achromat design. The differences between these designs can be found in the Objective Tutorial tab.
All of these objectives are suitable for brightfield microscopy, and all but the RMS100X-O are suitable for DIC microscopy. Additionally, the RMS60X-PFOD and RMS100X-PFOD objectives feature a built-in iris diaphragm, which is designed to be partially closed during darkfield microscopy in order to preserve the darkness of the background. This is absolutely necessary for high numerical aperture (above NA = 1.2) oil immersion objectives when using an oil immersion darkfield condenser. For ordinary brightfield observations, the iris diaphragm should be left fully open. The iris diaphragm adjustment is pictured above and to the right.
These objectives use standard RMS threading. To use these objectives with a different thread standard, please see our RMS Thread Adapters.
Objective manufacturers recommend using immersion oils from the same manufacturer for best performance; Thorlabs offers a variety of immersion oils below. A protective cap is also available for these objectives; see below for details.

- Oil Immersion Objectives for the Visible Spectrum
- Infinity-Corrected, Plan Fluorite Design
- Ideal for High-NA Imaging
- M25 x 0.75 Threading
- Designed for a Tube Lens Focal Length of 200 mm
- 60 mm Parfocal Length
This objective provides 100X magnification, features high transmission, particularly at UV wavelengths, and produces flat images across the field of view, making this objective well suited for use in laser scanning microscopy. It is designed for DIC microscopy, but can also be utilized for brightfield microscopy, fluorescence, and polarized light microscopy. The high NA of this objective also makes it suitable for Optical Tweezer applications. These objectives use M25 x 0.75 threading, which can be converted to other thread standards using Thorlabs' selection of M25 x 0.75 adapters.
This objective is designed for use from -18 °C to 60 °C (0 °F to 140 °F) and is not recommended for use at extreme temperatures. Objective manufacturers recommend using immersion oils from the same manufacturer for best performance; Thorlabs offers a variety of immersion oils below.

- Oils for Use with Oil Immersion Objectives
- Very Low Autofluorescence Oils are Optimized for Fluorescence Microscopy
- Non-Drying and Polychlorinated Biphenyl (PCB) Free
These Microscope Immersion Oils are designed for use with Oil Immersion Microscope Objectives. Placing an oil medium between the front surface of the objective and the cover glass allows the objective to achieve a high numerical aperture, maximizing light collection by the objective. To minimize refraction of light from the sample, the refractive indices of immersion oils are very close to those of cover glass.
Immersion oils are available with low or very low autofluorescence. Autofluorescence is the natural fluorescence emission of the oil when exposed to light. Each immersion oil has a different level of background emission, which either increases or decreases the contrast of the image; oils with very low autofluorescence are optimized for use in sensitive or UV fluorescence microscopy applications.
To clean immersion objectives after use with immersion oils, use a soft optical cleaning tissue such as our MC-5 premium lens tissues.
| Item # | MOIL-30 | MOIL-20LN | OILCL30 | MOIL-10LF | ||
|---|---|---|---|---|---|---|
| Refractive Indexa | 1.518 at 546.1 nm | |||||
| Abbe Numbera (at 546.1 nm) | 40.8 | 42.1 | 41 | 45.8 | ||
| Type | Olympus Type F | Leica Type N | Cargille Type LDF | Leica Type F | ||
| Viscositya,b | 450 mm2/s | 825 mm2/s | 500 mm2/s | 435 mm2/s | ||
| Autofluorescence | Low | Low | Very Low | Very Low | ||
| Volume | 30 mL / 28 g | 20 mL | 30 mL | 10 mL | ||
 Products Home
Products Home























 Zoom
Zoom

 Microscope Objectives, Oil Immersion
Microscope Objectives, Oil Immersion