Does it matter whether a beam expander or reducer has a Keplerian or Galilean design?

The design of the beam expander or reducer does not always matter to the application, but the choice can be influenced by factors such as the easier alignment and more intuitive design of the Keplerian devices and the compact dimensions of the Galilean devices. Additionally, a Keplerian device focuses the light between its two lenses and then outputs an inverted beam. A Galilean device maintains the orientation of the beam and provides the option to select lenses to reduce the amount of spherical aberration in the output beam.

Beam expanders and reducers are typically used only with collimated beams, rather than diverging beams, and these designs take their inspiration from Keplerian and Galilean telescopes. The magnification provided in both cases equals the focal length of the output lens divided by the focal length of the input lens.

Click to Enlarge

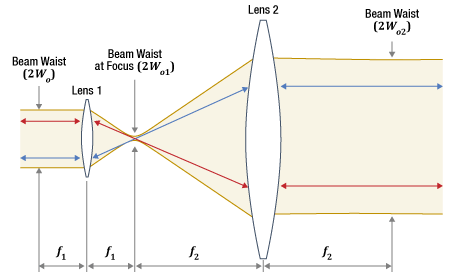
Figure 1: The simplest Keplerian beam expander or reducer includes two positive lenses. The focal lengths of Lens 1 and Lens 2 are f₁ and f₂, respectively. The lenses are separated by a distance equal to the sum of their focal lengths (f₁ + f₂), and the output beam is inverted relative to the input beam. 

Click to Enlarge

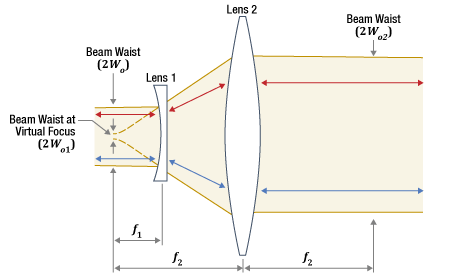
Figure 2: A basic Galilean beam expander or reducer includes a negative lens with focal length (f₁) and a positive lens with focal length (f₂). The lenses are positioned so that the distance between them equals the difference in their focal lengths (f₂ - f₁). Galilean designs do not focus the light between the two lenses, maintain the beam orientation, and are shorter than Keplerian designs.

Characteristics of the Keplerian Design
In the simplest Keplerian design, two positive lenses are separated by a distance equal to the sum of their focal lengths (Figure 1). A design based on the Keplerian telescope will never be shorter than the sum of the two lenses' focal lengths, and the output beam is inverted with respect to the input beam. 

The beam comes to a focus between the two lenses. This provides the opportunity to spatially filter the beam. For example, a pinhole filter could be placed at the beam's focal point to improve beam quality. Away from the focus, the beam diameter expands as it approaches the output lens. To increase the diameter of the collimated beam provided by the output lens, it is necessary to move the output lens farther away from the focus. Since the distance between the focus and the output lens equals the focal length, this requires using a lens with a longer focal length.

The Keplerian design is typically not preferred for high-energy beams, such as the high-power pulsed laser beams used in some cutting and other manufacturing applications. Focusing pulses with nanosecond duration and optical powers around ~1 MW or higher, for example, can ionize the air and create a spark, which undesirably reduces the power of the pulse and can negatively affect the beam quality. 

Characteristics of the Galilean Design
A basic Galilean telescope also includes two lenses, but one is negative while the other is positive (Figure 2). The lenses are positioned so that the distance between them equals the difference in their focal lengths, resulting in a more compact design than the Keplerian approach. 

The Galilean approach can also be used to minimize the spherical aberration induced by the beam expander or reducer. All spherical lenses introduce spherical aberration, and one consequence is the spread of the beam focus along the optical axis. In the case of a positive spherical lens, parallel rays incident closer to the lens' outer perimeter focus to a point on the optical axis closer to the lens, compared with parallel rays incident near the lens' center. Since a negative spherical lens has the opposite effect, the negative lens in the Galilean design can be used to cancel out some of the spherical aberration induced by the positive lens.

When the device is used as a beam expander, the smaller-diameter beam is incident on the negative lens. The diverging beam provided by the negative lens increases in diameter as it approaches the positive lens, instead of focusing between the two lenses. This diverging beam can be described as having a virtual focus, which is located on the opposite side of the negative lens, as shown in Figure 2. Since the positive lens is one focal length (f₂) away from this virtual focus, the positive lens outputs a collimated beam that is not inverted when compared with the input beam. If the beam is not rotationally symmetric, the beam's output orientation may be important to the application. 

Expansion Ratio
Beam expanders and reducers are designed to accept and provide collimated beams. Although the beams are collimated, their diameters change as they propagate due to the effects of diffraction. Ideally, the input beam waist is positioned one focal length away from the input lens as shown in Figures 1 and 2. The output beam waist is then one focal length away from the output lens. If the input beam waist is not one focal length away from the input lens, the location of the output beam waist, the output beam waist diameter, and/or the divergence of the output beam may not match estimated values.

Both the beam's waist diameter (2W_o ) and divergence angle (θ ) are affected by beam expanders and reducers. The change to these two beam parameters can be estimated using the device's beam expansion ratio (m ). The output beam waist diameter is calculated by multiplying the beam expansion ratio and the input beam diameter. The output beam's divergence angle is calculated by dividing the input beam's divergence angle by the beam expansion ratio.

When the device includes two lenses, the formula for calculating the beam expansion ratio is the same for both Keplerian and Galilean designs. The beam expansion ratio equals the focal length of the output lens divided by the focal length of the input lens. The devices shown in Figures 1 and 2 are beam expanders when the light is incident on Lens 1, whose focal length is f₁. In this case, the second lens (Lens 2) has focal length f₂ and the beam expansion ratio (m₁₂) is

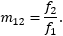
If the devices in Figures 1 and 2 are used as beam reducers, the light is incident from the opposite direction, upon Lens 2. Then, Lens 1 is the output lens, and the beam expansion ratio becomes m₂₁ , which is f₁ divided by f₂.