When does NA provide a good estimate of the fiber's acceptance angle?

Click to Enlarge

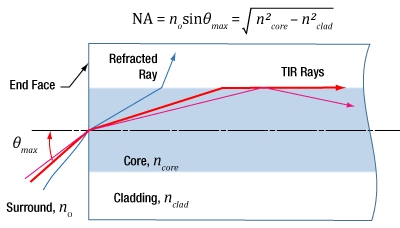
Figure 1: Rays incident at angles ≤θ_max will be captured by the cores of multimode fiber, since these rays experience total internal reflection (TIR) at the interface between core and cladding. A requirement for TIR is that n_core > n_clad .

Click to Enlarge

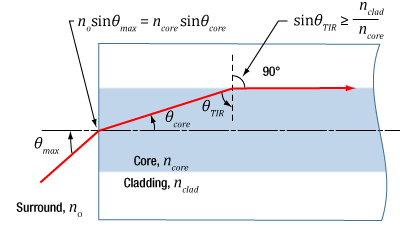
Figure 2: The behavior of the ray at the boundary between the core and cladding, which depends on their refractive indices, determines whether the ray incident on the end face is coupled into the core. The equation for NA can be found using geometry and the two equations noted at the top of this figure. 

Numerical aperture (NA) provides a good estimate of the maximum acceptance angle for most multimode fibers, as shown in Figure 1. This relationship should not be used for single mode fibers.

Acceptance Angle and NA
In the ray model of light, a ray's angle of incidence determines whether or not it will be coupled into the fiber's core. The cutoff angle is the maximum acceptance angle (θ_max ), which is related to the NA (Figure 1).

Rays with an angle of incidence ≤θ_max are totally internally reflected (TIR) at the boundary between the fiber's core and cladding. As these rays propagate down the fiber, they remain trapped in the core.

Rays with angles of incidence larger than θ_max refract at and pass through the interface between the core and cladding. This light may travel in the cladding for a while but is eventually lost from the fiber. 

Geometry Defines the Relationship
The relationship between NA and θ_max can be found using the geometry diagrammed in Figure 2. Snell's law was used at both interfaces, and the substitution sin(90°) = 1 was made. This geometry illustrates the most extreme conditions under which TIR will occur at the boundary between the core and cladding. 

The refractive indices of the core and cladding, n_core  and n_clad , respectively, play a key role. In order for TIR to occur, n_core must be larger than n_clad . The greater their difference, the larger the NA and maximum acceptance angle.

Angles of Incidence and Fiber Modes
When the angle of incidence is ≤θ_max , the incident light ray is coupled into one of the multimode fiber's guided modes. Generally speaking, the lower the angle of incidence, the lower the order of the excited fiber mode. Lower-order modes concentrate most of their intensity near the center of the core. The lowest order mode is excited by rays incident normally on the end face.

Single Mode Fibers are Different
In the case of single mode fibers, the ray model in Figure 2 is not useful, and the calculated NA (acceptance angle) does not equal the maximum angle of incidence or describe the fiber's light gathering ability.

Single mode fibers have only one guided mode, the lowest order mode, which is excited by rays with 0° angles of incidence. However, calculating the NA results in a nonzero value. The ray model also does not accurately predict the divergence angles of the light beams successfully coupled into and emitted from single mode fibers. The beam divergence occurs due to diffraction effects, which are not taken into account by the ray model but can be described using the wave optics model. The Gaussian beam propagation model can be used to calculate beam divergence with high accuracy.