How is the polarization ellipse related to the polarization state?

Click to Enlarge

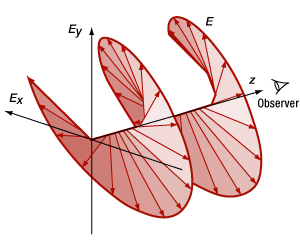
Figure 2: As the electric field () propagates, the tip of the vector follows a helical path. In this case, propagation is along the z-axis, and the helicity of the path followed by the  vector is positive (clockwise rotation).

Click to Enlarge

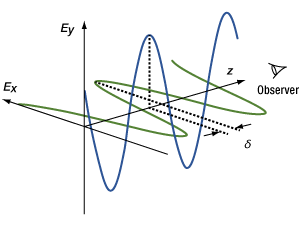
Figure 1: The electric field () can be expressed as the sum of two orthogonal components (E_x and E_y ), with a phase shift (δ ) between them.

Click to Enlarge

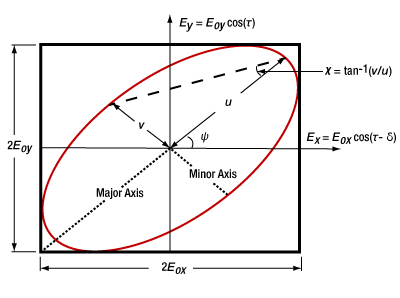
Figure 3: If an observer looks into the beam propagating from the origin in Figure 2, the tip of the rotating electric field vector traces out an ellipse. The ellipse can be described in terms of angles Ψ and χ. The equations in this figure use (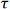) to represent ( 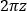/λ - ωt ), where λ is the material-dependent wavelength, ω is frequency, and t is time.

The polarization ellipse is a way to visualize the polarization state.

As a laser beam propagates, the tip of its electric field vector moves along a three dimensional path determined by the polarization state. If an observer looking into the beam could see the electric field advancing in real time, the vector's tip would appear to cycle around the propagation axis while following a two-dimensional, elliptical track.

The shape of this track is the polarization ellipse, which becomes a line for linearly polarized light and a circle for circularly polarized light.

Components of Light
The electric field vector () can be described by its orthogonal components, E_x and E_y . Figure 1 illustrates a case of elliptically polarized light, in which the polarization is not linear or circular. The E_x and E_y components have different amplitudes, and the phase difference (δ ) between the E_x and E_y  components is not an integer multiple of 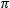/2. The E_x and E_y components' values increase and decrease periodically, but they vary out of sync with one another and span different ranges.

If the orthogonal components were added together as vectors, the total field vector would rotate around the propagation axis as it traveled (Figure 2), and its length would vary with the rotation angle. Looking into the beam, perpendicular to the E_x - E_y plane, the tip of the vector would trace out the curve of the polarization ellipse (Figure 3).

Polarization Ellipse
An observer looking into the beam will describe a different polarization ellipse than an observer facing the opposite direction. Due to this, it is necessary to specify the direction the observer faces. Here, the observer is assumed to be looking into the beam.

The polarization ellipse is bound by a rectangle whose sides are equal to twice the amplitudes, E_ox and E_oy , of the E_x and E_y components, respectively. This rectangle provides information about the fraction of the light contained in each orthogonal component.

To determine the specific characteristics of the polarization ellipse corresponding to a polarization state, the phase delay between the E_x  and E_y  components must also be considered. Key characteristics of the ellipse providing polarization state information are the rotation of the major axis with respect to the E_x axis and the relative lengths of the minor and major axes.

The angle (ψ ) between the major axis of the ellipse and the E_x axis is known by many names, including orientation angle, angle of inclination, rotation, tilt, and azimuth. It varies between -90° and 90°, and it is ±45° when E_ox and E_oy have equal magnitudes.

The ellipticity of the polarization ellipse is the ratio (ε ) between the lengths of the minor and major axes. Since the orientation is typically stated as an angle, it can be convenient to also express ellipticity as an angle ( χ ). The ellipticity has a range of values from zero ( χ = 0°) for linearly polarized light, which is the case for δ = 0, to one ( χ = 45°) for circularly polarized light, which is the case for δ = 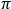/2.

The tip of the electric field vector may rotate in a right-hand (clockwise) or left-hand (counterclockwise) direction as it propagates. This is known as the handedness or helicity of light, in which right-hand polarized light has positive helicity and left-hand polarized light has negative helicity. The direction can be determined using values of the E vector at time equal to zero (E_t=0 ) and at a time one quarter of a period (T ) later (E_t=T/4 ). If the cross product (E_t=0 x E_t=T/4 ) points in the direction of beam propagation, the rotation is counterclockwise (left handed). If not, the rotation of the E-field vector is clockwise (right handed).  

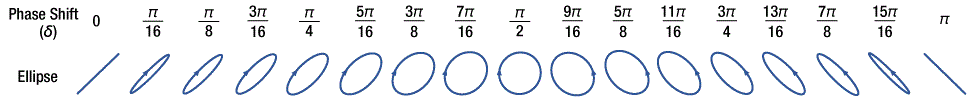
Click for Details 

Figure 4: The ellipticity and orientation of the polarization ellipse provides information about the phase shift (δ ) between the E_x and E_y components of the electric field. The ellipses shown above result when the peak amplitudes of both components are the same. The direction of the E vector's rotation is indicated by the direction of the arrow on the polarization ellipse. Click the image to see ellipticity and orientation angles for each case.