Numerical Aperture is not a Good Parameter for Single Mode Fibers


Please Wait
Does NA provide a good estimate of beam divergence from a single mode fiber?
Significant error can result when the numerical aperture (NA) is used to estimate the cone of light emitted from, or that can be coupled into, a single mode fiber. A better estimate is obtained using the Gaussian beam propagation model to calculate the divergence angle. This model allows the divergence angle to be calculated for whatever beam spot size best suits the application.
Since the mode field diameter (MFD) specified for single mode optical fibers encloses ~86% of the beam power, this definition of spot size is often appropriate when collimating light from and focusing light into a single mode fiber. In this case, to a first approximation and when measured in the far field,
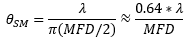 , , |
(1) |
is the divergence or acceptance angle (θSM ), in radians. This is half the full angular extent of the beam, it is wavelength  )
)
| Rayleigh Range: | ||
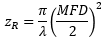 |
||
| Beam Radius at Distance z: | ||
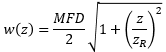 |
||
|
Figure 1: These curves illustrate the consequence of using NA to calculate the divergence (θSM ) of light output from a single mode fiber. Significant error in beam spot diameter can be avoided by using the Gaussian beam propagation model. This plot models a beam from SM980-5.8-125. The values used for NA and MFD were 0.13 and 6.4 µm, respectively. The operating wavelength was 980 nm, and the Rayleigh range was 32.8 µm. |
||
Gaussian Beam Approach
Although a diverging cone of light is emitted from the end face of a single mode optical fiber, this light does not behave as multiple rays travelling at different angles to the fiber's axis.
Instead, this light resembles and can be modeled as a single Gaussian beam. The emitted light propagates similarly to a Gaussian beam since the guided fiber mode that carried the light has near-Gaussian characteristics.
The divergence angle of a Gaussian beam can differ substantially from the angle calculated by assuming the light behaves as rays. Using the ray model, the divergence angle would equal sin-1(NA). However, the relationship between NA and divergence angle is only valid for highly multimode fibers.
Figure 1 illustrates that using the NA to estimate the divergence angle can result in significant error. In this case, the divergence angle was needed for a point on the circle enclosing 86% of the beam's optical power. The intensity of a point on this circle is a factor of 1/e2 lower than the peak intensity.
The equations to the right of the plot in Figure 1 were used to accurately model the divergence of the beam emitted from the single mode fiber's end face. The values used to complete the calculations, including the fiber's MFD, NA, and operating wavelength are given in the figure's caption. This rate of beam divergence assumes a beam size defined by the 1/e2 radius, is nonlinear for distances z < zR , and is approximately linear in the far field (z >> zR ).
The angles noted on the plot were calculated from each curve's respective slope. When the far field approximation given by Equation (1) is used, the calculated divergence angle is 0.098 radians (5.61°).
References
[1] Andrew M. Kowalevicz Jr. and Frank Bucholtz, Beam Divergence from an SMF-28 Optical Fiber (NRL/MR/5650--06-8996) (Naval Research Laboratory, Washington, DC, 2006).
|
Looking for more Insights? |
Date of Last Edit: Feb. 28, 2020 |
| Posted Comments: | |
Pat Harris
(posted 2022-09-28 12:37:31.553) I realize the question I'm asking may not have a straightforward answer but I'm looking for a sort of first approximation perspective. When launching a laser output from a multimode fiber and assuming the NA is used as the half angle beam divergence in radians where is the angle referenced? Is it in 1/e^2 or 1/e^3? Thank you very much for your time and consideration. pat jgreschler
(posted 2022-10-04 02:55:19.0) Thank you for reaching out to Thorlabs. For multimode fibers we define NA by calculation, as on this webpage: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=10417. I have reached out to you directly to discuss this application further. |
 Products Home
Products Home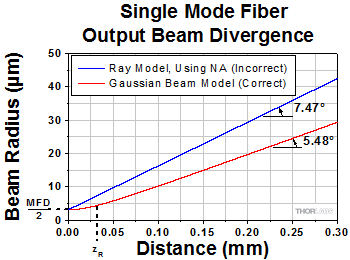
 NA is not a Good Parameter for SM Fiber
NA is not a Good Parameter for SM Fiber