What is needed to determine the direction and magnitude of the Faraday rotation angle?

An approach for determining the direction and magnitude of the Faraday rotation angle uses both linearly polarized input light and a magnetic field whose applied strength can be adjusted. Faraday rotation is a consequence of the Faraday effect, which causes the polarization orientation of linearly polarized light to rotate as it propagates through a material in the presence of a magnetic field. The Faraday rotation angle can be characterized by analyzing magnetic-field dependent measurements of the polarization orientation of the light output from the material. The angular difference between the polarization orientations of the light input to and output from the material is measured for each magnetic field strength value. This set of angular difference values can then be used to determine the Faraday rotation angle for a particular magnetic field strength, as is demonstrated using the example of a fixed-length CdMgTe crystal.

Click to Enlarge

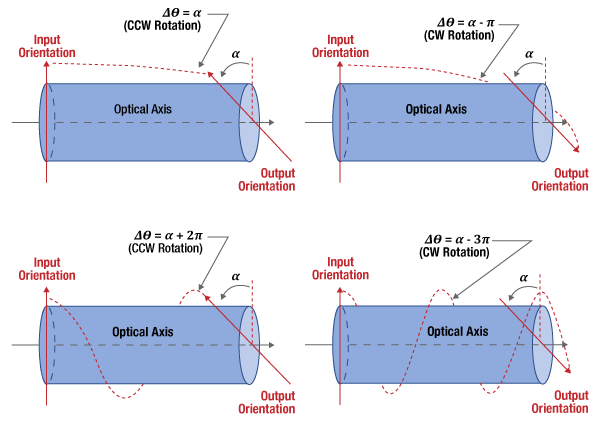
Figure 1: The Faraday effect causes linearly polarized light to rotate around the optical axis. The direction of rotation and the number of rotations depends on the applied magnetic field, the propagation direction of the light, and material properties. The direction and magnitude of the Faraday rotation (Δθ ) cannot be determined by measuring the angular difference () between polarization orientations of the light input to and output from the material, since these angles are mapped to an angular range between 0 and .

Click to Enlarge

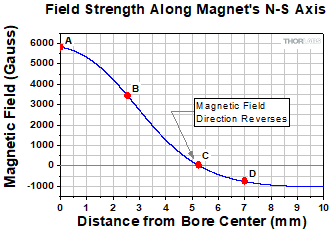
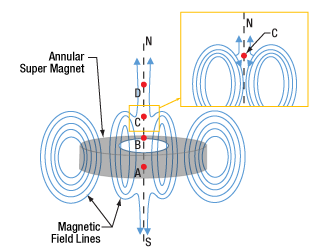
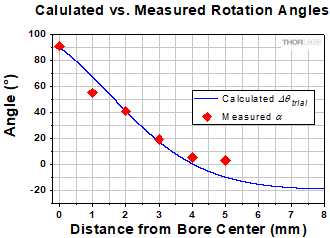
Figure 3: The magnetic field through the bore of the annular super magnet used in this work was calculated. The points labeled on this plot are also labeled in Figure 2. Point A corresponds to the center of the bore, and the field is zero at point C. The magnetic field strength is positive when it is directed towards the magnet's south pole.

Click to Enlarge

Figure 2: The annular super magnet used in this work is illustrated. The calculated magnetic field along the N-S axis is modeled in Figure 3. The magnetic field at points labeled in this image are indicated on the plot. At point C, the field lines cancel each other. The direction of the field also reverses at this point.

Click to Enlarge

Figure 4: Plotting the calculated angles (Δθ_trial ) and the measured angles () together is one way to visualize their relationship. The value of 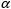measured for an applied magnetic field value of 5800 Gauss was used to calculate a constant (V^_trial ), which was then used to calculate Δθ_trial as described in the table. Since the Δθ_trial and measured 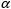values are in good agreement, the measured angles equal the Faraday rotation angles. 

Trial Verdet Constant Calculation (Vtrial )

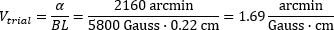Trial Faraday Rotation Calculation (Δθtrial )

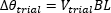Faraday Rotation Angle
The direction of the Faraday rotation around the optical axis depends on the orientation of the magnetic field (B ) and the sign of the material's intrinsic Verdet constant (V ). The Faraday rotation angle (Δθ ),

also depends on the propagation distance (L ) through the material under the influence of the applied magnetic field. By convention and from a perspective looking back towards the light source, when the beam propagates parallel to the magnetic field and the Verdet constant is positive, the rotation of the polarization vector is counter-clockwise (CCW) around the optical axis. The rotation is clockwise (CW) when the input light propagates in a direction opposite to the magnetic field. Faraday rotation angle measurements are often used to calculate the material's Verdet constant.

Measured Angle
A technique that compares the polarization orientations of the linearly polarized light input to, and output from, the material provides an angular value (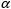). However, this approach automatically maps each angle to the range between 0 and 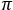, and neither the rotation direction, or the number of rotations the linearly polarized light made around the optical axis (Figure 1) is known.

Varying the Magnetic Field Strength
If values of 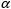 are measured for different applied magnetic fields, the Faraday rotation angle for a particular applied field can be determined. The applied field can be changed by moving the material to different positions within a static, but spatially varying, magnetic field.

For example, the magnetic field strength within the bore of an annular super magnet varies with distance along the N-S axis, while the field's direction remains parallel to the axis (Figures 2 and 3). The plot of the magnetic field in Figure 3 was calculated based on a model of the annular super magnet.

The magnetic field strength can be varied, without changing the field's direction, by translating the sample along the N-S axis. In this work, the sample was moved to specific points along this axis, and the position was measured with respect to the center of the magnet's bore. 

Characterizing the Faraday Rotation
A convenient starting point for characterizing the Faraday rotation angle is to assume values of 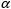, measured for different applied magnetic field values, have the same magnitude as the corresponding Faraday rotation angles. The next step is to test this assumption.

This procedure was followed to determine the direction and magnitude of the Faraday rotation angle when a magnetic field is applied to a 0.22 cm long CdMgTe crystal. An annular super magnet provided the magnetic field, and values of 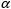were calculated for measurements made with the crystal placed at various points along the N-S axis. The crystal was moved between the points A and C labeled in Figure 2. Within this range, the light propagates along the direction of the magnetic field. After point C, the magnetic field direction reverses.

A trial Verdet constant (V_trial , table) was calculated using the value of 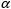(2160 arcmin) and the corresponding magnetic field strength (5800 Gauss). Then trial Faraday rotation angles (Δθ_trial , table) were calculated using V_trial . Since the measured and the modeled data are in good agreement (Figure 4), the measured values of 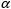are equal to the Faraday rotation angles. The differences between the calculated and measured angles are attributed mostly to differences between the modeled and actual magnetic fields, although measurement error may also contribute. The data plotted in Figure 4 indicate the sign of the calculated Verdet constant is positive, as well as establish that 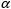can be used in the equation to calculate an accurate value of the Verdet constant.

When the two sets of angular data do not agree, the actual Faraday rotation angle is the sum of the measured 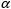angle value and a factor of 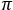. A special case is when the measured 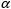angles and the calculated trial Faraday rotation angles both have the same magnitude, but their signs are opposite. The two angles then differ by 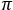and the actual and trial Verdet constants have opposite signs.