Mounted Quartz Zero-Order Achromatic Wave Plates

- Flat Retardance Over Broad Wavelength Ranges
- Low Reflectance and Beam Deviation
- Mounted Quarter- and Half-Wave Plates with Ø10 mm or Ø22.6 mm Clear Aperture
AHWP10M-600
Ø1" Mounted Quartz Achromatic Half-Wave Plate
Fast Axis Indicated
on Housing
AQWP05M-340
Ø1/2" Mounted Quartz Achromatic Quarter-Wave Plate
Application Idea
Wave Plate Mounted in
PRM1 Rotation Mount

Please Wait
| Common Specificationsa | ||
|---|---|---|
| Product Series | AQWP05M or AHWP05M | AQWP10M or AHWP10M |
| Clear Aperture | Ø10.0 mm (Ø0.39") | Ø22.6 mm (Ø0.89") |
| Mounted Diameter | 25.4 mm (1.00") | 30.5 mm (1.20") |
Click to Enlarge
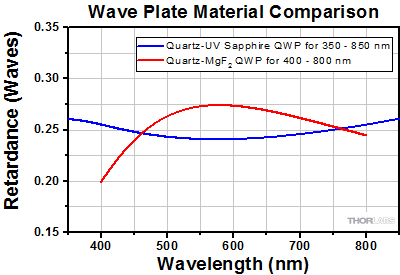
This plot compares the theoretical performance for two of our achromatic quarter-wave plates. The wave plate made from quartz and UV sapphire (AQWP05M-580) provides a flatter spectral response over the operating range than the wave plate made from quartz and magnesium fluoride (AQWP05M-600). See the blue info icons (
Features
- Spectrally Flat Retardance
- Operating Ranges from UV to Beyond Telecom Wavelengths
- AR Coatings for 260 - 410 nm, 350 - 850 nm, 400 - 800 nm, 690 - 1200 nm, or 1100 - 2000 nm
- Air-Spaced Design Provides High Damage Thresholds
- Quarter- and Half-Wave Plates Available
- Constructed by Aligning Crystalline Quartz Plates with Either Magnesium Fluoride or UV Sapphire Plates
- Custom Options Available, Please Contact Tech Sales for More Information
Thorlabs' Quartz Zero-Order Achromatic Wave Plates are constructed by aligning the fast axis of a birefringent quartz plate with the slow axis of another birefringent plate made from magnesium fluoride or UV sapphire, resulting in a relative phase delay of λ/4 or λ/2 between the two axes. The use of crystalline quartz with magnesium fluoride or UV sapphire minimizes the wavelength dependence of the retardation such that a nearly flat spectral response is achieved over the entire operating range of the achromatic wave plate (see the example retardance graph to the right). This allows these achromatic wave plates to be used over much broader wavelength ranges than our multi-order quartz wave plates. These wave plates are designed for use at normal incidence.
These achromatic wave plates are available in two sizes. The smaller versions feature a Ø10 mm clear aperture and come in an unthreaded anodized aluminum housing with a Ø25.4 mm diameter. This housing is compatible with SM1-threaded (1.035"-40) rotation mounts if an SM1RR retaining ring is used to hold the housing in place. In contrast, the larger versions have a clear aperture of Ø22.6 mm and are mounted in SM1-threaded lens tubes. These lens tubes can be directly threaded into rotation mounts or other rigid optomechanical parts. In each version, the anodized aluminum housing includes an engraving that indicates the orientation of the fast axis of the wave plate, its intended wavelength range, and type (λ/4 or λ/2).
Our achromatic wave plates are assembled by placing an etched stainless steel spacing ring between two birefringent plates and epoxying the three pieces together. Adhesive is only applied outside of the clear aperture of the wave plate. The fast axis is marked on the three-piece assembly with a line, in addition to being engraved on the housing. If desired, the wave plate can be removed from its housing for use in custom or OEM applications; see the blue info icons (![]() ) below for the unmounted diameter and thickness. Once removed, realigning the wave plate to this line on the assembly can be challenging; contact Tech Support if you would like Thorlabs to realign the wave plate as a complimentary service. Thorlabs can also produce custom wave plates with no AR coating, a different AR coating, or a different design wavelength than those offered below. For further information on using and selecting a wave plate, please see the Selection Guide tab or contact Tech Sales.
) below for the unmounted diameter and thickness. Once removed, realigning the wave plate to this line on the assembly can be challenging; contact Tech Support if you would like Thorlabs to realign the wave plate as a complimentary service. Thorlabs can also produce custom wave plates with no AR coating, a different AR coating, or a different design wavelength than those offered below. For further information on using and selecting a wave plate, please see the Selection Guide tab or contact Tech Sales.
| Wave Plate Selection Guide | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Quartz Zero-Order Achromatic | Polymer Zero-Order Achromatic | Superachromatic | Quartz Zero-Order Half-Wave |
Quartz Zero-Order Quarter-Wave |
Polymer Zero-Order Half-Wave |
Polymer Zero-Order Quarter-Wave |
Low-Order | Multi-Order | Dual Wavelength | Telecom | Polarization Optics |
Operating Principle of Wave Plates
Optical wave plates are constructed from birefringent materials that have a difference in refractive index between two orthogonal axes. This birefringent property introduces a velocity difference between light polarized along the fast and slow principal axes of the wave plate. The fast principal axis of the wave plate has a lower refractive index, resulting in a faster velocity for light polarized in this direction. Conversely, the slow axis has a higher refractive index, resulting in a slower velocity for light with this polarization. When light passes through a wave plate, this velocity difference leads to a phase difference between the two orthogonal polarization components. The actual phase shift depends on the properties of the material, the thickness of the wave plate, and the wavelength of the signal, and can be described as:
![]()
where n1 is the refractive index along the slow axis, n2 is the refractive index along the orthogonal fast axis, d is the thickness of the wave plate, and λ is the signal wavelength.
Using a Wave Plate
Wave plates are typically available with a retardance of λ/4 or λ/2, meaning that a phase shift of a quarter wavelength or a half a wavelength (respectively) is created.
Half-Wave
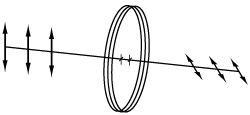
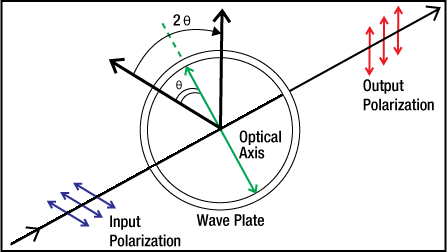
As described above, a wave plate has two principal axes: fast and slow. Each axis has a different refractive index and, therefore, a different wave velocity. When a linearly polarized beam is incident on a half-wave plate, and the polarization of this beam does not coincide with one of these axes, the output polarization will be linear and rotated with respect to the polarization of the input beam (see image at right). When applying a circularly polarized beam, a clockwise (counterclockwise) circular polarization will transform into a counterclockwise (clockwise) circular polarization.
Half-wave (λ/2) plates are typically used as polarization rotators. Mounted on a rotation mount, a λ/2 wave plate can be used as a continuously adjustable polarization rotator, as shown below. Additionally, when used in conjunction with a Polarizing Beamsplitter a λ/2 wave plate can be used as a variable ratio beamsplitter.
The angle between the output polarization and the input polarization will be twice the angle between the input polarization and the wave plate’s axis (see diagram to the lower right). When the polarization of the input beam is directed along one of the axes of the wave plate, the polarization direction will remain unchanged.
Quarter-Wave
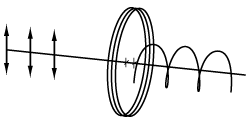
A quarter-wave plate is designed such that the phase shift created between the fast and slow axes is a quarter wavelength (λ/4). If the input beam is linearly polarized with the polarization plane aligned at 45° to the wave plate's fast or slow axis, then the output beam will be circularly polarized (see image at right). If the linearly polarized beam is aligned at an angle other than 45°, then the output will be elliptically polarized. Conversely, the application of a circularly polarized beam to a λ/4 wave plate results in a linearly polarized output beam. Quarter wave plates are used in Optical Isolators, optical pumps, and EO Modulators.

Click to Enlarge
Figure 1: Top Images (a,b): Engraving Reflects Updated Assembly Process as of October 2018; Bottom Images (c,d): Past Engraving
Fast and Slow Axis Identification
In October 2018, Thorlabs updated its wave plate assembly process and associated product engravings to be consistent with the IEEE/SPIE convention (see the Polarization Handedness Tutorial) for determining the fast and slow axes. By this convention, the current revisions of wave plates have the fast axis denoted by the “FAST AXIS” engraving visible in Figure 1 to the right. Although the location of the axes and the retardation value for each wave plate is easily determined, differentiating between the fast and slow axes is far more involved.
For most applications, the knowledge of whether an axis is fast or slow is not nearly as important as the retardation value. However, the fast/slow difference determines the left/right-hand circular polarization of light output from a quarter-wave plate, which can be important in applications such as atomic and solid state physics spectroscopy. To ensure the accuracy of our labeling moving forward, we have incorporated several redundant testing setups into our production processes, as described below.
Test Setup 1: Reflection Off Uncoated Metal with n > 1
This test setup is based on the method of Petre Logofatu1, which is also summarized well by Galgano and Henriques2. In this method, a light source passes through a generator, which is a linear polarizer oriented at 45° to the horizontal. Then, the light passes through the wave plate sample under test (SUT), is reflected off an uncoated metal surface (any metal with n > 1 will suffice), and passes through an analyzer (a second linear polarizer oriented at 90° to the generator). The light is then measured by a power sensor.
Our setup, shown in Figure 2 to the right, used a HeNe laser as the light source, two GTH10M-A Glan-Taylor polarizers as the generator and analyzer, a custom uncoated stainless steel reflective surface, an S120C power sensor, and a PM100D power meter console. A full parts list, except the custom metal surface and SUT, is provided below Figure 2.
As described by Logofatu, the power reflection coefficient, R in the equation below, can be derived from the Fresnel equations, showing that there will be a large difference in reflection off the metal depending on whether the fast or the slow axis of the SUT is horizontal.
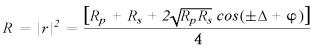
Here, Rp and Rs represent the p-polarized and s-polarized components of R, Δ is the retardance of the SUT, and φ is the phase difference between the p and s reflection coefficients of the metallic surface. From this, we can determine which axis we would expect a higher reflection value when horizontal, and compare expected values to experimental values. Using a large angle of incidence allows for a large separation between s and p coefficients. This correlates with high versus low measured reflection, enabling easy determination of fast versus slow axis. As in both papers, the test was performed at a variety of angles. The results were then fitted to a theoretical curve.
The equation for R shown above differs from that in the Logofatu reference, in which we identified an error; our Reflection Coefficient Derivation PDF shows our own derivation of the Logofatu result.

Click to Enlarge
Figure 3: Low Coherence Interferometry Wave Plate Testing Setup
Test Setup 2: Low Coherence Interferometry
This test setup uses low coherence interferometry to measure the optical path length (OPL) of the SUT as it is rotated, where the longest OPL corresponds with the slow axis, and the shortest OPL corresponds with the fast axis. This method is additionally verified by modifying the reference arm of the interferometer, adding a reference window and specular back surface to allow for calculation of the group index (ngSUT) along and normal to the crystal axis. These values can then be compared to known values, assuring the reliability of this test.
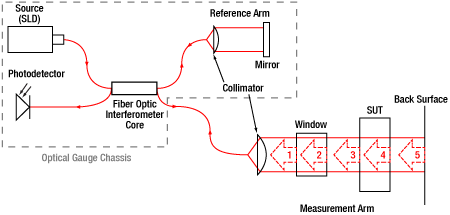
Our setup, shown in Figure 3 to the right, used a modified Bristol 157 Series Optical Gauge. As can be seen in Figure 4 below, the majority of the low coherence interferometer is contained within the chassis of the optical gaugea. The measurement arm is then modified with Thorlabs components, such that the fiber output can be aligned with a low NA objective, passed through a LPNIR100 linear polarizer and partially reflected off a WG11010 reference window, all mounted on a 34 mm rail. The light then reflects off the SUT and a custom specular back surface to send the interferometric signal back to the optical gauge.
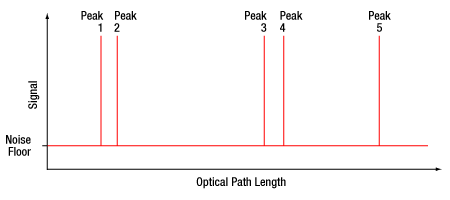
The additional reference surfaces and resulting physical thickness are used to double check the validity of the results. This is done with a quick calculation to determine the group index of both the fast and slow axes. Figure 5 shows a qualitative representation of the output produced by this setup. Peaks 1 and 2 are created by the reference window, Peaks 3 and 4 by the SUT wave plate, while Peak 5 is generated by the reference surface. Thickness data from peak to peak are calculated by the software and output into a table. By first taking the distance from Peak 2 to Peak 5 before the wave plate is inserted, the total physical thickness, Tair0, is obtainedb. When inserting the wave plate, we can then take the distance from Peak 2 to 3, Tair1, and Peak 4 to 5, Tair2. Using this information we can easily calculate the thickness of the wave plate, TSUT by subtracting Tair1 and Tair2 from Tair0. Measuring the distance from Peak 3 to Peak 4 would give us OPLSUT. Dividing OPLSUT by TSUT produces the group index of the SUT, ngSUT. Comparing this group index to that provided in literature for quartz3 or MgF24 both along and normal to the crystal axis, we are in good agreement.
Click to Enlarge
Figure 4: Example Low Coherence Interferometry Diagram;
Numbered reflections in the measurement arm correspond with peak numbers in Figure 5.
Click to Enlarge
Figure 5: Representation of Output from Optical Gauge
| Damage Threshold Specifications | |
|---|---|
| Coating Designation (Item # Suffix) |
Damage Threshold |
| -340 | 2.5 J/cm2 (266 nm, 10 ns, 10 Hz, Ø0.218 mm) 5 J/cm2 (355 nm, 10 ns, 10 Hz, Ø0.200 mm) |
| -580 | 7.5 J/cm2 (532 nm, 10 ns, 10 Hz, Ø0.200 mm) |
| -600 | 5 J/cm2 (532 nm, 10 ns, 10 Hz, Ø0.489 mm) |
| -980 | 0.432 J/cm2 (797 nm, 180 fs, 1 kHz, Ø0.178 mm) 5 J/cm2 (810 nm, 10 ns, 10 Hz, Ø0.157 mm) |
| -1600 | 5 J/cm2 (1542 nm, 10 ns, 10 Hz, Ø0.189 mm) |
Damage Threshold Data for Thorlabs' Mounted Achromatic Wave Plates
The specifications to the right are measured data for Thorlabs' mounted achromatic wave plates. Damage threshold specifications are constant for a given coating type, regardless of the size or order of the wave plate.
Laser Induced Damage Threshold Tutorial
The following is a general overview of how laser induced damage thresholds are measured and how the values may be utilized in determining the appropriateness of an optic for a given application. When choosing optics, it is important to understand the Laser Induced Damage Threshold (LIDT) of the optics being used. The LIDT for an optic greatly depends on the type of laser you are using. Continuous wave (CW) lasers typically cause damage from thermal effects (absorption either in the coating or in the substrate). Pulsed lasers, on the other hand, often strip electrons from the lattice structure of an optic before causing thermal damage. Note that the guideline presented here assumes room temperature operation and optics in new condition (i.e., within scratch-dig spec, surface free of contamination, etc.). Because dust or other particles on the surface of an optic can cause damage at lower thresholds, we recommend keeping surfaces clean and free of debris. For more information on cleaning optics, please see our Optics Cleaning tutorial.
Testing Method
Thorlabs' LIDT testing is done in compliance with ISO/DIS 11254 and ISO 21254 specifications.
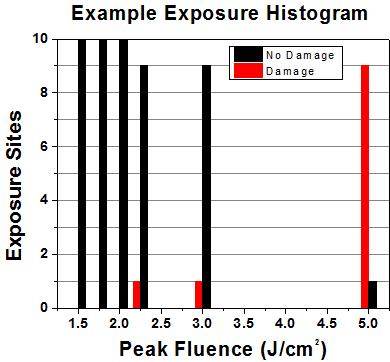
First, a low-power/energy beam is directed to the optic under test. The optic is exposed in 10 locations to this laser beam for 30 seconds (CW) or for a number of pulses (pulse repetition frequency specified). After exposure, the optic is examined by a microscope (~100X magnification) for any visible damage. The number of locations that are damaged at a particular power/energy level is recorded. Next, the power/energy is either increased or decreased and the optic is exposed at 10 new locations. This process is repeated until damage is observed. The damage threshold is then assigned to be the highest power/energy that the optic can withstand without causing damage. A histogram such as that below represents the testing of one BB1-E02 mirror.

The photograph above is a protected aluminum-coated mirror after LIDT testing. In this particular test, it handled 0.43 J/cm2 (1064 nm, 10 ns pulse, 10 Hz, Ø1.000 mm) before damage.
| Example Test Data | |||
|---|---|---|---|
| Fluence | # of Tested Locations | Locations with Damage | Locations Without Damage |
| 1.50 J/cm2 | 10 | 0 | 10 |
| 1.75 J/cm2 | 10 | 0 | 10 |
| 2.00 J/cm2 | 10 | 0 | 10 |
| 2.25 J/cm2 | 10 | 1 | 9 |
| 3.00 J/cm2 | 10 | 1 | 9 |
| 5.00 J/cm2 | 10 | 9 | 1 |
According to the test, the damage threshold of the mirror was 2.00 J/cm2 (532 nm, 10 ns pulse, 10 Hz, Ø0.803 mm). Please keep in mind that these tests are performed on clean optics, as dirt and contamination can significantly lower the damage threshold of a component. While the test results are only representative of one coating run, Thorlabs specifies damage threshold values that account for coating variances.
Continuous Wave and Long-Pulse Lasers
When an optic is damaged by a continuous wave (CW) laser, it is usually due to the melting of the surface as a result of absorbing the laser's energy or damage to the optical coating (antireflection) [1]. Pulsed lasers with pulse lengths longer than 1 µs can be treated as CW lasers for LIDT discussions.
When pulse lengths are between 1 ns and 1 µs, laser-induced damage can occur either because of absorption or a dielectric breakdown (therefore, a user must check both CW and pulsed LIDT). Absorption is either due to an intrinsic property of the optic or due to surface irregularities; thus LIDT values are only valid for optics meeting or exceeding the surface quality specifications given by a manufacturer. While many optics can handle high power CW lasers, cemented (e.g., achromatic doublets) or highly absorptive (e.g., ND filters) optics tend to have lower CW damage thresholds. These lower thresholds are due to absorption or scattering in the cement or metal coating.

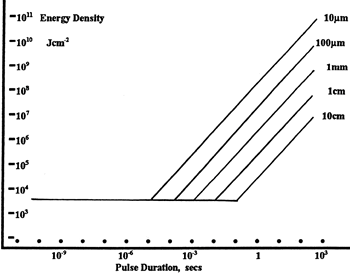
LIDT in linear power density vs. pulse length and spot size. For long pulses to CW, linear power density becomes a constant with spot size. This graph was obtained from [1].
Pulsed lasers with high pulse repetition frequencies (PRF) may behave similarly to CW beams. Unfortunately, this is highly dependent on factors such as absorption and thermal diffusivity, so there is no reliable method for determining when a high PRF laser will damage an optic due to thermal effects. For beams with a high PRF both the average and peak powers must be compared to the equivalent CW power. Additionally, for highly transparent materials, there is little to no drop in the LIDT with increasing PRF.
In order to use the specified CW damage threshold of an optic, it is necessary to know the following:
- Wavelength of your laser
- Beam diameter of your beam (1/e2)
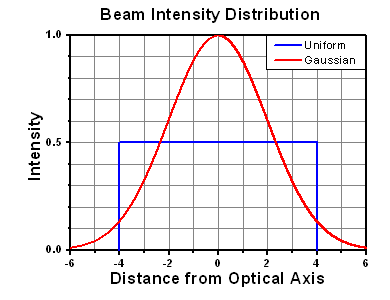
- Approximate intensity profile of your beam (e.g., Gaussian)
- Linear power density of your beam (total power divided by 1/e2 beam diameter)
Thorlabs expresses LIDT for CW lasers as a linear power density measured in W/cm. In this regime, the LIDT given as a linear power density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size, as demonstrated by the graph to the right. Average linear power density can be calculated using the equation below.
The calculation above assumes a uniform beam intensity profile. You must now consider hotspots in the beam or other non-uniform intensity profiles and roughly calculate a maximum power density. For reference, a Gaussian beam typically has a maximum power density that is twice that of the uniform beam (see lower right).
Now compare the maximum power density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately. A good rule of thumb is that the damage threshold has a linear relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 10 W/cm at 1310 nm scales to 5 W/cm at 655 nm):

While this rule of thumb provides a general trend, it is not a quantitative analysis of LIDT vs wavelength. In CW applications, for instance, damage scales more strongly with absorption in the coating and substrate, which does not necessarily scale well with wavelength. While the above procedure provides a good rule of thumb for LIDT values, please contact Tech Support if your wavelength is different from the specified LIDT wavelength. If your power density is less than the adjusted LIDT of the optic, then the optic should work for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. The damage analysis will be carried out on a similar optic (customer's optic will not be damaged). Testing may result in additional costs or lead times. Contact Tech Support for more information.
Pulsed Lasers
As previously stated, pulsed lasers typically induce a different type of damage to the optic than CW lasers. Pulsed lasers often do not heat the optic enough to damage it; instead, pulsed lasers produce strong electric fields capable of inducing dielectric breakdown in the material. Unfortunately, it can be very difficult to compare the LIDT specification of an optic to your laser. There are multiple regimes in which a pulsed laser can damage an optic and this is based on the laser's pulse length. The highlighted columns in the table below outline the relevant pulse lengths for our specified LIDT values.
Pulses shorter than 10-9 s cannot be compared to our specified LIDT values with much reliability. In this ultra-short-pulse regime various mechanics, such as multiphoton-avalanche ionization, take over as the predominate damage mechanism [2]. In contrast, pulses between 10-7 s and 10-4 s may cause damage to an optic either because of dielectric breakdown or thermal effects. This means that both CW and pulsed damage thresholds must be compared to the laser beam to determine whether the optic is suitable for your application.
| Pulse Duration | t < 10-9 s | 10-9 < t < 10-7 s | 10-7 < t < 10-4 s | t > 10-4 s |
|---|---|---|---|---|
| Damage Mechanism | Avalanche Ionization | Dielectric Breakdown | Dielectric Breakdown or Thermal | Thermal |
| Relevant Damage Specification | No Comparison (See Above) | Pulsed | Pulsed and CW | CW |
When comparing an LIDT specified for a pulsed laser to your laser, it is essential to know the following:
LIDT in energy density vs. pulse length and spot size. For short pulses, energy density becomes a constant with spot size. This graph was obtained from [1].
- Wavelength of your laser
- Energy density of your beam (total energy divided by 1/e2 area)
- Pulse length of your laser
- Pulse repetition frequency (prf) of your laser
- Beam diameter of your laser (1/e2 )
- Approximate intensity profile of your beam (e.g., Gaussian)
The energy density of your beam should be calculated in terms of J/cm2. The graph to the right shows why expressing the LIDT as an energy density provides the best metric for short pulse sources. In this regime, the LIDT given as an energy density can be applied to any beam diameter; one does not need to compute an adjusted LIDT to adjust for changes in spot size. This calculation assumes a uniform beam intensity profile. You must now adjust this energy density to account for hotspots or other nonuniform intensity profiles and roughly calculate a maximum energy density. For reference a Gaussian beam typically has a maximum energy density that is twice that of the 1/e2 beam.
Now compare the maximum energy density to that which is specified as the LIDT for the optic. If the optic was tested at a wavelength other than your operating wavelength, the damage threshold must be scaled appropriately [3]. A good rule of thumb is that the damage threshold has an inverse square root relationship with wavelength such that as you move to shorter wavelengths, the damage threshold decreases (i.e., a LIDT of 1 J/cm2 at 1064 nm scales to 0.7 J/cm2 at 532 nm):
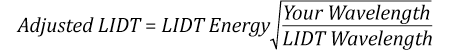
You now have a wavelength-adjusted energy density, which you will use in the following step.
Beam diameter is also important to know when comparing damage thresholds. While the LIDT, when expressed in units of J/cm², scales independently of spot size; large beam sizes are more likely to illuminate a larger number of defects which can lead to greater variances in the LIDT [4]. For data presented here, a <1 mm beam size was used to measure the LIDT. For beams sizes greater than 5 mm, the LIDT (J/cm2) will not scale independently of beam diameter due to the larger size beam exposing more defects.
The pulse length must now be compensated for. The longer the pulse duration, the more energy the optic can handle. For pulse widths between 1 - 100 ns, an approximation is as follows:
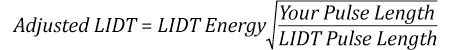
Use this formula to calculate the Adjusted LIDT for an optic based on your pulse length. If your maximum energy density is less than this adjusted LIDT maximum energy density, then the optic should be suitable for your application. Keep in mind that this calculation is only used for pulses between 10-9 s and 10-7 s. For pulses between 10-7 s and 10-4 s, the CW LIDT must also be checked before deeming the optic appropriate for your application.
Please note that we have a buffer built in between the specified damage thresholds online and the tests which we have done, which accommodates variation between batches. Upon request, we can provide individual test information and a testing certificate. Contact Tech Support for more information.
[1] R. M. Wood, Optics and Laser Tech. 29, 517 (1998).
[2] Roger M. Wood, Laser-Induced Damage of Optical Materials (Institute of Physics Publishing, Philadelphia, PA, 2003).
[3] C. W. Carr et al., Phys. Rev. Lett. 91, 127402 (2003).
[4] N. Bloembergen, Appl. Opt. 12, 661 (1973).
In order to illustrate the process of determining whether a given laser system will damage an optic, a number of example calculations of laser induced damage threshold are given below. For assistance with performing similar calculations, we provide a spreadsheet calculator that can be downloaded by clicking the LIDT Calculator button. To use the calculator, enter the specified LIDT value of the optic under consideration and the relevant parameters of your laser system in the green boxes. The spreadsheet will then calculate a linear power density for CW and pulsed systems, as well as an energy density value for pulsed systems. These values are used to calculate adjusted, scaled LIDT values for the optics based on accepted scaling laws. This calculator assumes a Gaussian beam profile, so a correction factor must be introduced for other beam shapes (uniform, etc.). The LIDT scaling laws are determined from empirical relationships; their accuracy is not guaranteed. Remember that absorption by optics or coatings can significantly reduce LIDT in some spectral regions. These LIDT values are not valid for ultrashort pulses less than one nanosecond in duration.

Figure 71A A Gaussian beam profile has about twice the maximum intensity of a uniform beam profile.
CW Laser Example
Suppose that a CW laser system at 1319 nm produces a 0.5 W Gaussian beam that has a 1/e2 diameter of 10 mm. A naive calculation of the average linear power density of this beam would yield a value of 0.5 W/cm, given by the total power divided by the beam diameter:
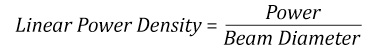
However, the maximum power density of a Gaussian beam is about twice the maximum power density of a uniform beam, as shown in Figure 71A. Therefore, a more accurate determination of the maximum linear power density of the system is 1 W/cm.
An AC127-030-C achromatic doublet lens has a specified CW LIDT of 350 W/cm, as tested at 1550 nm. CW damage threshold values typically scale directly with the wavelength of the laser source, so this yields an adjusted LIDT value:

The adjusted LIDT value of 350 W/cm x (1319 nm / 1550 nm) = 298 W/cm is significantly higher than the calculated maximum linear power density of the laser system, so it would be safe to use this doublet lens for this application.
Pulsed Nanosecond Laser Example: Scaling for Different Pulse Durations
Suppose that a pulsed Nd:YAG laser system is frequency tripled to produce a 10 Hz output, consisting of 2 ns output pulses at 355 nm, each with 1 J of energy, in a Gaussian beam with a 1.9 cm beam diameter (1/e2). The average energy density of each pulse is found by dividing the pulse energy by the beam area:
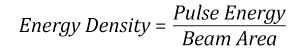
As described above, the maximum energy density of a Gaussian beam is about twice the average energy density. So, the maximum energy density of this beam is ~0.7 J/cm2.
The energy density of the beam can be compared to the LIDT values of 1 J/cm2 and 3.5 J/cm2 for a BB1-E01 broadband dielectric mirror and an NB1-K08 Nd:YAG laser line mirror, respectively. Both of these LIDT values, while measured at 355 nm, were determined with a 10 ns pulsed laser at 10 Hz. Therefore, an adjustment must be applied for the shorter pulse duration of the system under consideration. As described on the previous tab, LIDT values in the nanosecond pulse regime scale with the square root of the laser pulse duration:
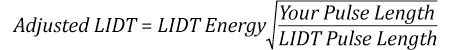
This adjustment factor results in LIDT values of 0.45 J/cm2 for the BB1-E01 broadband mirror and 1.6 J/cm2 for the Nd:YAG laser line mirror, which are to be compared with the 0.7 J/cm2 maximum energy density of the beam. While the broadband mirror would likely be damaged by the laser, the more specialized laser line mirror is appropriate for use with this system.
Pulsed Nanosecond Laser Example: Scaling for Different Wavelengths
Suppose that a pulsed laser system emits 10 ns pulses at 2.5 Hz, each with 100 mJ of energy at 1064 nm in a 16 mm diameter beam (1/e2) that must be attenuated with a neutral density filter. For a Gaussian output, these specifications result in a maximum energy density of 0.1 J/cm2. The damage threshold of an NDUV10A Ø25 mm, OD 1.0, reflective neutral density filter is 0.05 J/cm2 for 10 ns pulses at 355 nm, while the damage threshold of the similar NE10A absorptive filter is 10 J/cm2 for 10 ns pulses at 532 nm. As described on the previous tab, the LIDT value of an optic scales with the square root of the wavelength in the nanosecond pulse regime:
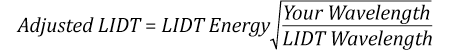
This scaling gives adjusted LIDT values of 0.08 J/cm2 for the reflective filter and 14 J/cm2 for the absorptive filter. In this case, the absorptive filter is the best choice in order to avoid optical damage.
Pulsed Microsecond Laser Example
Consider a laser system that produces 1 µs pulses, each containing 150 µJ of energy at a repetition rate of 50 kHz, resulting in a relatively high duty cycle of 5%. This system falls somewhere between the regimes of CW and pulsed laser induced damage, and could potentially damage an optic by mechanisms associated with either regime. As a result, both CW and pulsed LIDT values must be compared to the properties of the laser system to ensure safe operation.
If this relatively long-pulse laser emits a Gaussian 12.7 mm diameter beam (1/e2) at 980 nm, then the resulting output has a linear power density of 5.9 W/cm and an energy density of 1.2 x 10-4 J/cm2 per pulse. This can be compared to the LIDT values for a WPQ10E-980 polymer zero-order quarter-wave plate, which are 5 W/cm for CW radiation at 810 nm and 5 J/cm2 for a 10 ns pulse at 810 nm. As before, the CW LIDT of the optic scales linearly with the laser wavelength, resulting in an adjusted CW value of 6 W/cm at 980 nm. On the other hand, the pulsed LIDT scales with the square root of the laser wavelength and the square root of the pulse duration, resulting in an adjusted value of 55 J/cm2 for a 1 µs pulse at 980 nm. The pulsed LIDT of the optic is significantly greater than the energy density of the laser pulse, so individual pulses will not damage the wave plate. However, the large average linear power density of the laser system may cause thermal damage to the optic, much like a high-power CW beam.
| Posted Comments: | |
Gwan Woo Lee
(posted 2025-05-02 01:27:15.233) Is the red pencil mark on the optic itself indicating the fast axis? mgarodia
(posted 2025-05-06 02:42:57.0) Thank you for reaching out to us. Yes, the edge marking on the optic indicates the fast axis. Zhaoran Xu
(posted 2025-04-10 10:03:50.093) I wonder about the retardance of AQWP05M-600 from 800 to 1000nm. Thank you. cdolbashian
(posted 2025-04-22 12:45:34.0) Thank you for reaching out to us with this inquiry! I have contacted you directly to share such extended data with you. Charles Stark
(posted 2025-02-27 13:27:29.193) Dear Tholabs,
I am curious whether the datasheet for the achromatic 350 - 850 QWP is correct when it mentions that group delay is on the order of 17 ps. This seems incredibly long for a thin Quartz plate? Do these waveplates really not function with fs pulses? EGies
(posted 2025-02-28 01:02:08.0) Thank you for contacting Thorlabs. The AQWP05M-580 is constructed by aligning the fast axis of a multi-order quartz waveplate with the slow axis of a multi-order UV sapphire waveplate, resulting in a relative phase delay of λ/4 between the two axes. The waveplates together have a total thickness of approximately 3mm, resulting in the larger than expected group delay. In comparison to the other AQWP05M waveplates, the AQWP05M-580 does use thicker plates in its construction. I have reached out to you directly regarding the requirements of your particular application. Zihao Zhao
(posted 2024-12-06 03:18:19.927) Dose this wave plate has a limited AOI(angle of incident)? Can it work at AOI from -45° to +45°? Because AOI in my light path varies in this range. Thank you. blarowe
(posted 2024-12-06 09:48:09.0) Thank you for contacting Thorlabs. The AOI will have a significant impact on the retardance of these waveplates, so use at angles other than normal will not match retardance specs. Our polymer zero order waveplates will be less sensitive to changes in AOI, though they will still be impacted. I have reached to you directly with more information. Rafael Barros
(posted 2024-04-26 11:07:35.74) Hello, could you please provide data on the AQWP05M-980 for an extender wavelength range, as for example 500-1600nm?
Thank you in advance cdolbashian
(posted 2024-05-06 03:37:17.0) Thank you for reaching out to us with this request for extended data. I have reached out to you directly to share such extended data. sangjun kim
(posted 2023-07-04 10:24:10.49) The delivery time is the most important factor. If we were to order three of these products, when could we expect to receive them? We appreciate your prompt response. cdolbashian
(posted 2023-07-21 02:55:01.0) Thank you for reaching out to us with this inquiry. Depending on your region the shipping will be different. I would recommend reaching out to your local Thorlabs sales office or distributor. Local sales locations can be found here: https://www.thorlabs.com/locations.cfm Marcela Mireles
(posted 2023-01-26 08:57:49.477) I'm curious to know if you could provide ellipticity of the output light? Thanks. jgreschler
(posted 2023-01-26 11:57:51.0) Thank you for reaching out to Thorlabs. The ellipticity of the output light will depend on the polarization state of the input light. I have reached out to you directly to discuss this application. entian song
(posted 2022-12-05 11:58:51.08) There seems to be a little contamination on the wave plate. I want to know what to use and how to clean it cdolbashian
(posted 2022-12-15 02:27:43.0) Thank you for reaching out to us with this inquiry Entian. This can be cleaned with standard cleaning methods which are outlined here: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=9025 user
(posted 2022-08-23 12:46:10.053) Can you offer customized achromatic quarter-wave plates with a larger clear aperture (>35 mm) in SM2-threaded mounts (like the WPQ20ME plates) for 400 to 800 nm? Pavel Bulkin
(posted 2021-12-22 06:03:40.553) On the product page of AQWP10M-580 it is written "The fast axis is marked on the three-piece assembly in pencil, in addition to being engraved on the housing." Before I take 3-piece assembly out of housing can you, maybe, indicate, where exactly I shall look for it? To have a photo of un-mounted QWP of this type with mark will be very useful!
Thank you very much in advance for your answer!
Pavel cdolbashian
(posted 2022-01-25 04:38:36.0) Thank you for reaching out to us Pavel! For these waveplates, there is a small machined flat around the perimeter of the circular optic. The fast axis is perpendicular to this flat edge. Wentao Hu
(posted 2021-10-19 21:28:40.657) what is the power handling capability and damage threshold of this waveplate? YLohia
(posted 2021-12-22 04:19:58.0) Please see the "Damage Thresholds" tab for the pulsed damage thresholds. Unfortunately, we don't specify the CW damage thresholds for these parts. Andriy Chmyrov
(posted 2021-06-08 09:46:59.867) Is it possible to supplement the transmission and the retardance data for the AHWP05M-980 for the spectral range 1200-1300 nm? Then it would cover the whole tuning range of popular dual-output ultrafast lasers such as Spectra-Physics InSight X3 and Coherent Discovery NX. YLohia
(posted 2021-06-09 02:10:45.0) Hello, I have reached out to you with theoretical extended range data. Zoran Sodnik
(posted 2020-12-14 08:34:40.987) It would be great to get an achromatic quarter wave plate with a usable spectrum that covers the InGaAs spectral range (900 nm - 1700 nm).
Best regards,
Zoran YLohia
(posted 2020-12-15 03:03:28.0) Hello Zoran, thank you for your feedback. We will consider offering such an item in the future. That being said, we do currently offer the SAQWP05M-1700 and FR600QM quarter waveplates to cover the InGaAs spectral range. user
(posted 2020-01-07 04:32:53.477) Dear Thorlabs support, Please provide the operating temperature range for AQWP10M-580 quarter wave plate. YLohia
(posted 2020-01-08 10:18:38.0) Hello, we use Devcon 5-minute epoxy for these waveplates, which is the limiting factor for the temperature range and has an operating temperature range of -40 to 200 degrees Fahrenheit. Wenzel Jakob
(posted 2019-03-18 12:41:46.71) Dear Thorlabs support, I'm trying to reconcile the supplementary information provided for the new AQWP10M-580 quarter wave plate. In particular, the AOI plot at 0 degrees (633nm) seems to disagree with the values shown in the retardation plot at 633nm. Can you clarify? nbayconich
(posted 2019-03-20 04:38:33.0) Thank you for bringing this to our attention. The correct retardance values are found in the retardance vs. wavelength section is about 0.2417 waves. We will update the AOI dependence plot to show the correct values. nadav3333
(posted 2018-12-01 09:16:13.82) Regarding the AQWP05M-980 quarter-wave plate - Is there any information on its' Transmission and Retardance for the wavelength range above 1200nm? say up to 1600-1700nm?
Thanks in advance! YLohia
(posted 2018-12-03 09:18:10.0) Hello, thank you for contacting Thorlabs. I'm reaching out to you directly with this extended range data. allanber
(posted 2018-11-06 04:46:29.44) do you have cw damage threshold value for AHWP05M-980? nbayconich
(posted 2018-11-19 03:09:04.0) Thank you for contacting Thorlabs. We have not yet performed formal CW laser induced damage threshold testing on these waveplates. If you can provide your operating wavelength, beam diameter & total power we can estimate whether or not your source will be suitable with this product.
A techsupport representative will reach out to you directly to discuss your application. wenzel.jakob
(posted 2018-03-16 15:08:12.917) One item that is conspicuously absent in this list is a hypothetical "AQWP10M-600", i.e. a visible light quarter-wave plate with 22mm clear aperture. Are there technical issues that prevent Thorlabs from manufacturing such an optic, or could this be created? YLohia
(posted 2018-03-30 11:57:51.0) Response from Yashasvi at Thorlabs USA: Hello, thank you for your feedback regarding this hypothetical product. You are correct, there are indeed technical issues preventing us from manufacturing this optic. The birefringent plates used to create the waveplate are quite thin for this large size and and impose manufacturing limitations. We may be able to offer an alternate solution and will reach out to you via email to discuss this possibility. m8ye
(posted 2018-01-18 09:16:20.21) Hi, can I buy the mirror in the AHWP05M-980, but not included the mount? Thanks. tfrisch
(posted 2018-01-19 02:56:52.0) Hello, thank you for contacting Thorlabs. I will reach out to you with a quote for the waveplate unmounted. alexandre.giuliani
(posted 2018-01-09 11:11:04.74) Hi, I would also like to see the retardation and transmission curves from 600 nm to 1400 nm.
Thank you. nbayconich
(posted 2018-01-12 01:27:14.0) Thank you for contacting Thorlabs. I will reach out to you directly with transmission & retardance data from 600nm to 1400nm. milan.delor
(posted 2017-09-13 10:50:47.433) Hi, I realize I'm not the first one to ask this on this feedback page, but you provide transmission and retardance data only down to 600 nm for the AHWP10M-600. Could you include data down to 400 nm? Many thanks! nbayconich
(posted 2017-09-25 11:15:47.0) Thank you for contacting Thorlabs. I will contact you directly with extended retardance and transmission plots for AHWP10M-600 up200403369
(posted 2017-07-19 17:05:47.82) Hello, I'm also interested in the retardance and transmission data for the AHWP05M-600 down to 350 nm. Thank you. nbayconich
(posted 2017-07-25 01:58:14.0) Thank you for contacting Thorlabs. I will contact you directly with extended retardance and transmission plots for AHWP05M-600. cwong3
(posted 2017-01-19 18:35:59.687) Can you provide retardance and transmission data for the AHWP05M-600 down to 350 nm? Thank you! tfrisch
(posted 2017-01-25 05:44:54.0) Hello, thank you for contacting Thorlabs. I will reach out to you with the data we have. user
(posted 2016-04-28 13:32:16.12) It refers one to the specification icon for the umounted thickness. Shouldn't you put a link to it in that sentence? I can't find the "specification" and I don't know what it looks like. Maybe instead of making me learn x to learn y just go ahead and link me to y. besembeson
(posted 2016-04-28 02:33:26.0) Response from Bweh at Thorlabs USA: The "Specifications" can be accessed by clicking on the "i" icon beside each of these waveplates. We will look into making this information clearer on the webpages. Please contact me at techsupport@thorlabs.com if you have further questions. minowa
(posted 2016-04-09 22:27:21.047) What is the cw damage threshold of AQWP05M-980? can i use it for the laser power density ~300W/cm^2 (3W and 0.9mm beam diameter). Thank you. besembeson
(posted 2016-04-11 04:00:42.0) Response from Bweh at Thorlabs USA: We don't have damage threshold specifications for CW yet but 3W at 0.9mm should be okay for the waveplate. Dong
(posted 2016-01-18 18:00:05.47) Achromatic waveplate is zero-order type as described in Overview tab. Is superachromatic waveplate also zero-order? besembeson
(posted 2016-01-20 05:06:05.0) Response from Bweh at Thorlabs USA: The superachromatic waveplates by the Pancharatnam design are not zero order. Dong
(posted 2016-01-18 17:55:44.377) Whats the difference between achromatic waveplate and super achromatic waveplate? Thanks. besembeson
(posted 2016-01-19 12:22:11.0) Response from Bweh at Thorlabs USA: Superachromatic waveplates exhibit much less dependence on wavelength than achromatic waveplates. The retardation of superachromatic waveplates is almost flat over a much broader spectrum. We have a graphical representation of the difference at the following link, under the "Overview" tab: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=2193 yahua.li
(posted 2014-10-15 01:51:14.467) From the web page, the wave plate of AHWP05M-1600 and AQHWP05M-1600 are designed for normal incident. When aligning with He-Ne laser, the reflection spot is shifting when rotating the wave plate. My question is how to align in laser cavity.
Thanks.
Yahua besembeson
(posted 2014-10-24 03:21:12.0) Response from Bweh: I think the issue might be the mount. I will follow up with you by email to determine what amount of deviation you are observing and to know which mount you are currently using. Other mounts to consider will be the kinamatic mount with vertical drive, VM1 (http://www.thorlabs.us/thorproduct.cfm?partnumber=VM1) or the Gimbal mirror mount, GM100 (http://www.thorlabs.us/thorproduct.cfm?partnumber=GM100). neel_leslie
(posted 2014-07-24 23:29:51.757) Can you provide the angle of incidence curve at 1340nm for the AHWP10M-1600? Also will this waveplate work at 1064? myanakas
(posted 2014-07-29 02:50:38.0) Response from Mike at Thorlabs: Thank you for your feedback. The waveplate will still work at 1064 nm though the retardance value will increase slightly from what is given at 1100 nm. I have contacted you directly with the AOI data at 1340 nm, measured transmission, and theoretical retardance data. We will look into updating the web page with this data. flickingerd
(posted 2014-07-07 18:34:17.32) Is the transmitted wavefront error spec for these optics PK-PK or RMS. I don't think it says, and would be forced to assume the worst (RMS) in this case. myanakas
(posted 2014-07-21 11:51:39.0) Response from Mike at Thorlabs: Thank you for your feedback. We are currently testing these optics to confirm peak-to-peak/RMS transmitted wavefront error. We will email and post the results on the website when we finish the measurements. guillaume.lepert07
(posted 2014-07-01 13:47:50.927) Hi, why can't we get a lambda/4 with 22.6mm clear aperture at 600nm ? It would be very useful. Thanks. jlow
(posted 2014-08-07 09:03:05.0) Response from Jeremy at Thorlabs: We have superachromatic wave plates available that provide flatter retardance which would be more useful for 600nm. If you are only working at 600nm, we can make zero order wave-plates for that exact wavelength as well. katonagabor89
(posted 2014-05-11 12:53:56.073) Could you sent me please the value of Group Delay Dispersion (GDD) of the waveplate AHWP05M-980?
Thank you very much. besembeson
(posted 2014-05-15 09:11:29.0) Response from Bweh E at Thorlabs: Thanks for contacting Thorlabs. For AHWP05M-980, GDD is about 75 fs^2. bkyang
(posted 2013-10-17 15:26:21.963) Can you please send me the retardation data of AQWP05M-600 from 360 nm to 830 nm? jlow
(posted 2013-10-17 09:01:00.0) Response from Jeremy at Thorlabs: We will contact you directly to provide this information. MTLIU
(posted 2013-10-05 01:01:09.187) Can you please show me the retardation and transmission curves from 600 nm to 1400 nm? pbui
(posted 2013-10-10 15:20:00.0) Response from Phong at Thorlabs: We will contact you directly to provide extended performance data for our waveplates. b.steel1
(posted 2013-03-27 12:51:30.39) Could you provide information (eg the specs page you have for most other items) on the retardance as a function of wavelength for the achromatic waveplates please?
We are wanting a 1/4 wave plate for a 550-1000 light source, and will probably choose between the 400-800 or 690-1200 passbands as 'good enough'. sharrell
(posted 2013-03-27 09:27:00.0) Response from Sean at Thorlabs: Thank you for contacting us. We recently added "Info Icon" pop-up spec tables that contain the retardance vs. wavelength plots and downloadable data. These can be found in the gray tables immediately above the ordering areas. rpsmith
(posted 2013-02-05 16:17:14.22) Hello,
I would like to use the HWP for ultrafast laser pulses in the 500-800nm regime. Do you have any information regarding the dispersion introduced by transmitting through such an optic?
Sincerely,
Ryan cdaly
(posted 2013-02-14 11:21:00.0) Response from Chris at Thorlabs: Thank you for using our web feedback. For the achromatic waveplates, the dispersion will be quite low. We anticipate along the lines of 50 fs^2 throughout the entire optic. jlow
(posted 2012-09-27 11:35:00.0) Response from Jeremy at Thorlabs: This was not a simple shift from Ø1/2" to Ø1". Due to thickness issues, we are exploring use of other materials for these parts. There is a good deal of development left with this project and unfortunately we cannot give an accurate time frame for release at this time. jonas.ries
(posted 2012-09-24 16:52:23.0) When will the AQP10-600 become available? That is an achromatic quater wave plate for visible light with 1" diameter? tcohen
(posted 2012-05-01 12:07:00.0) Response from Tim at Thorlabs: Thank you for your feedback. I have contacted you with data on the retardance vs AOI. f95941056
(posted 2012-04-27 06:15:36.0) Hi, I have one AHWP05M-1430, the former version of AHWP05M-1600. Can you provide the retardance vs. incident angle curve for this old product? Or the curve for AHWP05M-1600 is also OK. Thanks. utsavdeepak.dave
(posted 2012-04-11 10:30:12.0) Hi,
I wish to know if these Mounted Achromatic Waveplates are also offered with a 1" clear aperture. I am looking for a Quarter Wave Plate at 445 nm with at least 1" diameter, but a wide wavelength might be more useful in the future.
Thanks. bdada
(posted 2012-02-24 16:18:00.0) Response from Buki at Thorlabs to michael.renner:
Thank you for your feedback. We have sent you information about the retardation from 600nm to 2um. Please contact TechSupport@thorlabs.com if you have any questions. michael.renner
(posted 2012-01-09 13:08:28.0) I need a quarter-wave plate and a half-wave plate for the range from 900nm to 1600nm. Considering the anti-reflection coating I would go for the 980nm option. What about the retardation outside the specified range? What option would you recommend? Thank you! bdada
(posted 2012-01-03 17:47:00.0) Response from Buki at Thorlabs:
Thank you for your feedback. We are looking into providing more information on our retardation plots. In the meantime, please contact TechSupport@thorlabs.com if there is a particular waveplate you are interested in and we will get you an expanded plot. user
(posted 2012-01-03 19:43:18.0) It would be very helpful to have the retardation plots extend deyond the specified operating ranges and the applications don't always break nicely within the bands you have provided. I would suggest extending the plot so as to show the points at which the retardance changes by +/- 10% or at least 100 nm. bdada
(posted 2011-09-21 14:46:00.0) Response from Buki at Thorlabs:
We have contacted you with a graph showing the retardance outside the design wavelength. We will consider the best way to include this information on our website. peter.spencer00
(posted 2011-09-05 13:59:20.0) May I ask how the retardance of the 980 nm version of the quarter waveplate changes just outside its design wavelength range (i.e. from 1200 to 1400 nm for example)? jjurado
(posted 2011-06-21 19:40:00.0) Response from Javier at Thorlabs to zmeastman: Thank you very much for your feedback. We will look into generating this data and posting plots on the web for the dependence of the retardance as a function of the angle of incidence for our waveplates. In the meantime, I will send you this information directly. zmeastman
(posted 2011-06-20 16:43:30.0) It would be useful to have retardance versus angle of incidence data available for download for the complete line of wave plates. Customer Email: zmeastman@lucid-tech.com This customer would like to be contacted. user
(posted 2010-08-24 16:32:19.0) Tell Paul Melone at novaphase Happy Birthday, cant believe he is still kicking around! apalmentieri
(posted 2010-01-21 13:10:07.0) A response from Adam at Thorlabs to Joel: We are working on a 1" diameter, 22mm clear aperture design for these waveplates. Currently, we can provide this as a custom option for the 980 and 1600 versions. I will contact you directly to see if you are interested in a custom option. joel
(posted 2010-01-21 10:48:03.0) I need a larger aperture. Id buy these if they were available with a 1" aperture. Tyler
(posted 2008-06-12 10:02:55.0) A response from Tyler at Thorlabs to jpang and mthiel: All of the web presentations on wave plates now include the unmounted wave plate thickness. Thank you for taking the time to point out the need for this information. mthiel
(posted 2007-11-19 05:08:42.0) All mounted wave plates (achromatic, zero order, multi order) can be easily unmounted. jpang
(posted 2007-10-30 11:08:17.0) It would be good to have the thickness of the mounted and unmounted waveplate listed under specs tab.
Same applies to all the waveplates (zero order, multi-order and dual wavelength multi-order) |
Choosing a Wave Plate
Thorlabs offers achromatic, superachromatic, zero-order (both unmounted wave plates and mounted wave plates), low-order, and multi-order wave plates (single wavelength and dual wavelength) with either λ/4 or λ/2 phase shift.
Liquid Crystal Polymer (LCP) Zero-Order Achromatic Wave Plates provide phase retardance that is relatively independent of wavelength over a wide spectral range, while Quartz Zero-Order Achromatic Wave Plates perform similarly but with a higher surface quality, increased retardance accuracy, a smaller beam deviation, and a higher damage threshold. Superachromatic Wave Plates provide phase retardance almost entirely independent of wavelength over a much wider range than achromatic wave plates. In contrast, zero-order and multi-order wave plates without any chromatic correction provide a phase shift that is strongly wavelength dependent. Our achromatic polymer wave plates are designed for 450 - 700 nm, while our achromatic quartz wave plates are available with four operating ranges: 260 - 410 nm, 350 - 850 nm, 400 - 800 nm, 690 - 1200 nm, and 1100 - 2000 nm. Additionally, we offer superachromatic wave plates for the 310 - 1100 nm and 600 - 2700 nm ranges.
| Table 132A Zero-Order Wave Plate Comparison | ||||
|---|---|---|---|---|
| Chromatic Correction | Achromatic | None | ||
| Material | Quartz | LCP | Quartz | LCP |
| Sizes | Ø1/2" and Ø1" | Ø1/2" and Ø1" | Ø1/2", Ø1", and Ø2" | |
| Unmounted Versions Available | No | Yes | ||
| Mounted Versions Available | Yes | |||
| Retardances Available | 1/4 λ and 1/2 λ | |||
| Retardance Accuracy | <λ/300 | <λ/100 | <λ/300 | <λ/100 |
| Surface Quality | 20-10 Scratch-Dig | 60-40 Scratch-Dig | 20-10 Scratch-Dig | 60-40 Scratch-Dig |
| Coating | Broadband AR | V Coat | Broadband AR | |
| Coating Average Reflectance (per Surface) | <0.5%a | <0.5%a | <0.25%b | <1.0%a |
Zero-order wave plates are designed such that the phase shift created is exactly one quarter or one half of a wave. They offer substantially lower dependence on temperature and wavelength than multi-order wave plates. Our Zero-Order Quartz Half-Wave and Quarter-Wave Plates are composed of two wave plates stacked together with the fast axis of one aligned to the slow axis of the other to achieve zero-order performance. Thorlabs' zero-order wave plates are available for a number of discrete wavelengths ranging from 266 nm to 2020 nm. Our Polymer Zero-Order Half-Wave and Quarter-Wave Plates consist of a thin layer of liquid crystal polymer retarding material sandwiched between two glass plates and are available at discrete wavelengths between 405 nm and 2700 nm. Our quartz zero-order wave plates provide better retardance accuracy and lower reflectance (see Table 132A), while our LCP zero-order wave plates produce a smaller decrease in retardance at larger AOIs. In addition, Thorlabs also offers unmounted true Zero-Order Telecom Wave Plates for WDM applications.
MIR Wave Plates are made from a single piece of high-quality magnesium fluoride and provide either quarter-wave or half-wave retardance at 2.5 µm, 2.713 µm, 2.94 µm, 3.5 µm, 4.0 µm, 4.5 µm, or 5.3 µm. Light passing through these MIR wave plates will undergo a low number of full or partial wavelength shifts (also referred to as the order, or m) in addition to the fractional design retardance. This differs from true zero-order and multi-order wave plates which undergo no shift or a high number of shifts, respectively. The low-order design maintains near to true zero-order performance, making it a good alternative to true zero-order wave plates. The single magnesium fluoride substrate is also thinner compared to a zero-order design, which combines two multi-order wave plates, making our low-order retarders well suited for applications that are sensitive to dispersion.
Multi-Order Wave Plates are made such that the retardance of a light path will undergo a certain number of full wavelength shifts (also referred to as the order, or m) in addition to the fractional design retardance. Compared to their zero-order counterparts, the retardance of multi-order wave plates is more sensitive to wavelength and temperature changes. Multi-order wave plates are, however, a more economical solution for many applications where increased sensitivities are not an issue. Our multi-order wave plates are available for a number of discrete wavelengths ranging from 405 nm to 1550 nm. Thorlabs also offers Dual-Wavelength Multi-Order Wave Plates designed for use at both 532 nm and 1064 nm.
In addition to these options, Thorlabs also has the ability to design and manufacture custom wave plates for both OEM sales and individual low quantity orders. Our technical staff is able to help with all phases of your request: quoting, sales, and planning and manufacturing support. If you have a custom request or a question about our capabilities, please contact Tech Sales to start a discussion.

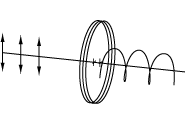
Quarter-wave plates can change linearly polarized light into circularly polarized light.

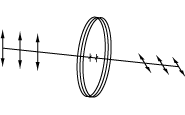
Half-wave plates can rotate the polarization plane of linearly polarized light.


Quarter-wave plates can change linearly polarized light into circularly polarized light.


Half-wave plates can rotate the polarization plane of linearly polarized light.
 Products Home
Products Home

















 Zoom
Zoom


 Quartz Achromatic Wave Plates
Quartz Achromatic Wave Plates