Dual Wavelength Multi-Order Wave Plates

- Operates as λ/2 @ λ1 & as λ/4 @ λ2
- Dual Wavelength Operation: 532 nm and 1064 nm
- Ø1/2" Waveplate Mounted in Ø1" Aluminum Mount
WPDM05M-1064H-532Q
WPDM05M-532H-1064Q
Wave Plate
Mounted in PRM1
Rotation Mount
Application Idea

Please Wait
| Click on the red Document icon next to the item numbers below to access the Zemax file download. Our entire Zemax Catalog is also available. |
Features
- Operates as a Quarter-Wave Plate at One Wavelength and a Half-Wave Plate at a Second Wavelength
- Dual V AR Coating: Ravg <0.25% at 532 nm and 1064 nm (0° AOI)
- Ø1/2" Waveplate Mounted in Ø1" Aluminum Mount
- Clear Aperture: Ø10 mm (Ø0.39")
- Custom Options Available, Please Contact Tech Support for More Information.
Thorlabs' dual wavelength, multi-order wave plates are made from high-quality crystalline quartz and are available at quarter-wave or half-wave retardance. The wave plates are designed to be used in dual wavelength setups (1064 nm and 532 nm) and operate as a quarter-wave plate at one wavelength and as a half-wave plate at the second wavelength. Two models are available: λ/4 @ 532 nm and λ/2 @ 1064 nm or a λ/4 @ 1064 nm and λ/2 @ 532 nm.
Multi-order refers to the fact that the retardance of a light path will undergo a certain number of full wavelength shifts (also referred to as the order, or m) in addition to the fractional design retardance. Compared to their zero-order counterparts, the retardance of multi-order wave plates are more sensitive to wavelength and temperature changes, however, they are less expensive and find use in many applications where the increased sensitivities is not an issue.
Our wave plates are mounted in a Ø1" housing with the fast axis of the wave plate clearly marked with a straight line on the housing's front panel. The wave plates are easily removed from their mounts for use in custom or OEM applications (see the Specs tab for the unmounted wave plate thickness). The unmounted waveplates have a small flat parallel to the fast axis (see image on the right). For further information on using and selecting a wave plate please visit our Wave Plate Selection Guide tab.
Thorlabs can also produce custom wave plates with no AR coating, a different AR coating, or a different design wavelength than those offered below. Please contact
Tech Support with inquiries.
| Wave Plate Selection Guide | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Achromatic | Superachromatic | Quartz Zero-Order Half-Wave |
Quartz Zero-Order Quarter-Wave |
Polymer Zero-Order Half-Wave |
Polymer Zero-Order Quarter-Wave |
Multi-Order | Dual Wavelength | Telecom | Polarization Optics |
| General Specifications | |
|---|---|
| Substrate | Crystalline Quartz |
| Operating Wavelengths | 532 nm & 1064 nm |
| Clear Aperture | Ø10 mm (Ø0.39") |
| Diameter | Unmounted: 12.7 mm ± 0.1 mm Mounted: 25.4 mm |
| Retardance Accuracy (Typical) | <λ/100 (Measured at 632.8 nm) |
| Reflectance | Dual V AR Coating: Ravg <0.25% at 532 nm and 1064 nm (0° AOI) |
| Transmitted Wavefront Error | <λ/10 |
| Beam Deviation | <10 arcsec |
| Surface Quality | 20-10 Scratch-Dig |
| Item # | Unmounted Wave Plate Nominal Thickness |
|---|---|
| WPDM05M-532H-1064Q | 1.1276532 mm |
| WPDM05M-1064H-532Q | 0.3038145 mm |
Operating Principle of Wave Plates
Optical wave plates are constructed from birefringent materials that have a difference in refractive index between two orthogonal axes. This birefringent property introduces a velocity difference between light polarized along the fast and slow principal axes of the wave plate. The fast principal axis of the wave plate has a lower refractive index, resulting in a faster velocity for light polarized in this direction. Conversely, the slow axis has a higher refractive index, resulting in a slower velocity for light with this polarization. When light passes through a wave plate, this velocity difference leads to a phase difference between the two orthogonal polarization components. The actual phase shift depends on the properties of the material, the thickness of the wave plate, and the wavelength of the signal, and can be described as:
![]()
where n1 is the refractive index along the slow axis, n2 is the refractive index along the orthogonal fast axis, d is the thickness of the wave plate, and λ is the signal wavelength.
Using a Wave Plate
Wave plates are typically available with a retardance of λ/4 or λ/2, meaning that a phase shift of a quarter wavelength or a half a wavelength (respectively) is created.
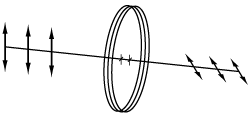
Half-Wave
As described above, a wave plate has two principal axes: fast and slow. Each axis has a different refractive index and, therefore, a different wave velocity. When a linearly polarized beam is incident on a half-wave plate, and the polarization of this beam does not coincide with one of these axes, the output polarization will be linear and rotated with respect to the polarization of the input beam (see image at right). When applying a circularly polarized beam, a clockwise (counterclockwise) circular polarization will transform into a counterclockwise (clockwise) circular polarization.
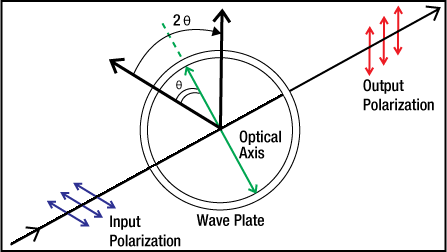
Half-wave (λ/2) plates are typically used as polarization rotators. Mounted on a rotation mount, a λ/2 wave plate can be used as a continuously adjustable polarization rotator, as shown below. Additionally, when used in conjunction with a Polarizing Beamsplitter a λ/2 wave plate can be used as a variable ratio beamsplitter.
The angle between the output polarization and the input polarization will be twice the angle between the input polarization and the wave plate’s axis (see diagram to the lower right). When the polarization of the input beam is directed along one of the axes of the wave plate, the polarization direction will remain unchanged.
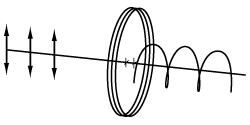
Quarter-Wave
A quarter-wave plate is designed such that the phase shift created between the fast and slow axes is a quarter wavelength (λ/4). If the input beam is linearly polarized with the polarization plane aligned at 45° to the wave plate's fast or slow axis, then the output beam will be circularly polarized (see image at right). If the linearly polarized beam is aligned at an angle other than 45°, then the output will be elliptically polarized. Conversely, the application of a circularly polarized beam to a λ/4 wave plate results in a linearly polarized output beam. Quarter wave plates are used in Optical Isolators, optical pumps, and EO Modulators.

Click to Enlarge
Figure 1: Top Images (a,b): Engraving Reflects Updated Assembly Process as of October 2018; Bottom Images (c,d): Past Engraving
Fast and Slow Axis Identification
In October 2018, Thorlabs updated its wave plate assembly process and associated product engravings to be consistent with the IEEE/SPIE convention (see the Polarization Handedness Tutorial) for determining the fast and slow axes. By this convention, the current revisions of wave plates have the fast axis denoted by the “FAST AXIS” engraving visible in Figure 1 to the right. Although the location of the axes and the retardation value for each wave plate is easily determined, differentiating between the fast and slow axes is far more involved.
For most applications, the knowledge of whether an axis is fast or slow is not nearly as important as the retardation value. However, the fast/slow difference determines the left/right-hand circular polarization of light output from a quarter-wave plate, which can be important in applications such as atomic and solid state physics spectroscopy. To ensure the accuracy of our labeling moving forward, we have incorporated several redundant testing setups into our production processes, as described below.
Test Setup 1: Reflection Off Uncoated Metal with n > 1
This test setup is based on the method of Petre Logofatu1, which is also summarized well by Galgano and Henriques2. In this method, a light source passes through a generator, which is a linear polarizer oriented at 45° to the horizontal. Then, the light passes through the wave plate sample under test (SUT), is reflected off an uncoated metal surface (any metal with n > 1 will suffice), and passes through an analyzer (a second linear polarizer oriented at 90° to the generator). The light is then measured by a power sensor.
Our setup, shown in Figure 2 to the right, used a HeNe laser as the light source, two GTH10M-A Glan-Taylor polarizers as the generator and analyzer, a custom uncoated stainless steel reflective surface, an S120C power sensor, and a PM100D power meter console. A full parts list, except the custom metal surface and SUT, is provided below Figure 2.
As described by Logofatu, the power reflection coefficient, R in the equation below, can be derived from the Fresnel equations, showing that there will be a large difference in reflection off the metal depending on whether the fast or the slow axis of the SUT is horizontal.
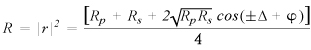
Here, Rp and Rs represent the p-polarized and s-polarized components of R, Δ is the retardance of the SUT, and φ is the phase difference between the p and s reflection coefficients of the metallic surface. From this, we can determine which axis we would expect a higher reflection value when horizontal, and compare expected values to experimental values. Using a large angle of incidence allows for a large separation between s and p coefficients. This correlates with high versus low measured reflection, enabling easy determination of fast versus slow axis. As in both papers, the test was performed at a variety of angles. The results were then fitted to a theoretical curve.
The equation for R shown above differs from that in the Logofatu reference, in which we identified an error; our Reflection Coefficient Derivation PDF shows our own derivation of the Logofatu result.

Click to Enlarge
Figure 3: Low Coherence Interferometry Wave Plate Testing Setup
Test Setup 2: Low Coherence Interferometry
This test setup uses low coherence interferometry to measure the optical path length (OPL) of the SUT as it is rotated, where the longest OPL corresponds with the slow axis, and the shortest OPL corresponds with the fast axis. This method is additionally verified by modifying the reference arm of the interferometer, adding a reference window and specular back surface to allow for calculation of the group index (ngSUT) along and normal to the crystal axis. These values can then be compared to known values, assuring the reliability of this test.
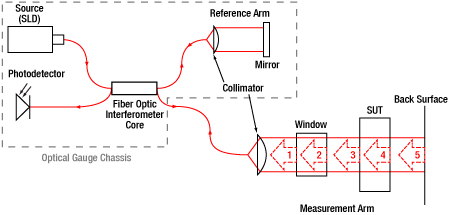
Our setup, shown in Figure 3 to the right, used a modified Bristol 157 Series Optical Gauge. As can be seen in Figure 4 below, the majority of the low coherence interferometer is contained within the chassis of the optical gaugea. The measurement arm is then modified with Thorlabs components, such that the fiber output can be aligned with a low NA objective, passed through a LPNIR100 linear polarizer and partially reflected off a WG11010 reference window, all mounted on a 34 mm rail. The light then reflects off the SUT and a custom specular back surface to send the interferometric signal back to the optical gauge.
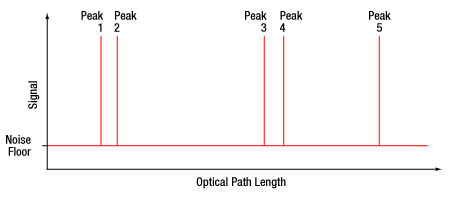
The additional reference surfaces and resulting physical thickness are used to double check the validity of the results. This is done with a quick calculation to determine the group index of both the fast and slow axes. Figure 5 shows a qualitative representation of the output produced by this setup. Peaks 1 and 2 are created by the reference window, Peaks 3 and 4 by the SUT wave plate, while Peak 5 is generated by the reference surface. Thickness data from peak to peak are calculated by the software and output into a table. By first taking the distance from Peak 2 to Peak 5 before the wave plate is inserted, the total physical thickness, Tair0, is obtainedb. When inserting the wave plate, we can then take the distance from Peak 2 to 3, Tair1, and Peak 4 to 5, Tair2. Using this information we can easily calculate the thickness of the wave plate, TSUT by subtracting Tair1 and Tair2 from Tair0. Measuring the distance from Peak 3 to Peak 4 would give us OPLSUT. Dividing OPLSUT by TSUT produces the group index of the SUT, ngSUT. Comparing this group index to that provided in literature for quartz3 or MgF24 both along and normal to the crystal axis, we are in good agreement.
Click to Enlarge
Figure 4: Example Low Coherence Interferometry Diagram;
Numbered reflections in the measurement arm correspond with peak numbers in Figure 5.
Click to Enlarge
Figure 5: Representation of Output from Optical Gauge
| Posted Comments: | |
srm37
(posted 2019-01-07 11:29:36.22) Dear sir/madam,
I was interested in these dual wavelength waveplates, but the system I'm using operates at 1050 nm and 515 nm. What performance quality would be expected using the waveplates as they are at those wavelengths?
Cheers,
Sam YLohia
(posted 2019-01-09 04:02:07.0) Hello Sam, thank you for contacting Thorlabs. As these are multi-order waveplates, unfortunately, the performance at non-design wavelengths is not optimal. I have reached out to you directly with data. klee
(posted 2009-09-25 11:53:12.0) A response from Ken at Thorlabs to olsonaj: We can do this as a special. We will send you a quotation by email. olsonaj
(posted 2009-09-25 01:20:00.0) This would be very useful if there was one that did 780nm and 1550 nm. (re: WPDM05M-1064H-532Q) |
Choosing a Wave Plate
Thorlabs offers achromatic, superachromatic, zero-order (both unmounted wave plates and mounted wave plates), low-order, and multi-order wave plates (single wavelength and dual wavelength) with either λ/4 or λ/2 phase shift.
Achromatic Wave Plates provide phase retardance that is relatively independent of wavelength over a wide spectral range, and Superachromatic Wave Plates provide phase retardance almost entirely independent of wavelength over a much wider range than achromatic wave plates. In contrast, zero-order and multi-order wave plates provide a phase shift that is strongly wavelength dependent. Our achromatic wave plates are available with four operating ranges: 260 - 410 nm, 350 - 850 nm, 400 - 800 nm, 690 - 1200 nm, and 1100 - 2000 nm. Additionally, we offer superachromatic wave plates for the 310 - 1100 nm and 600 - 2700 nm ranges.
| Round Zero-Order Wave Plate Comparison | ||
|---|---|---|
| Material | Quartz | LCP |
| Sizes | Ø1/2" and Ø1" | Ø1/2", Ø1", and Ø2" |
| Mounted Versions Available | Yes | Yes |
| Retardances Available | 1/4 λ and 1/2 λ | 1/4 λ and 1/2 λ |
| Retardance Accuracy | <λ/300 | <λ/100 |
| Surface Quality | 20-10 Scratch-Dig | 60-40 Scratch-Dig |
| Coating | V Coat | Broadband AR |
| Coating Reflectance (per Surface) |
0.25% | 0.5% Average Over Specified Coating Range |
Zero-order wave plates are designed such that the phase shift created is exactly one quarter or one half of a wave. They offer substantially lower dependence on temperature and wavelength than multi-order wave plates. Our Zero-Order Quartz Half-Wave and Quarter-Wave Plates are composed of two wave plates stacked together with the fast axis of one aligned to the slow axis of the other to achieve zero-order performance. Thorlabs' zero-order wave plates are available for a number of discrete wavelengths ranging from 266 nm to 2020 nm. Our Polymer Zero-Order Half-Wave and Quarter-Wave Plates consist of a thin layer of liquid crystal polymer retarding material sandwiched between two glass plates and are available at discrete wavelengths between 405 nm and 1550 nm. Our quartz zero-order wave plates provide better retardance accuracy and lower reflectance (see table), while our LCP zero-order wave plates produce a smaller decrease in retardance at larger AOIs. In addition, Thorlabs also offers unmounted true Zero-Order Telecom Wave Plates for WDM applications.
MIR Wave Plates are made from a single piece of high-quality magnesium fluoride and provide either quarter-wave or half-wave retardance at 2.5 µm, 3.5 µm, 4.0 µm, 4.5 µm, or 5.3 µm. Light passing through these MIR wave plates will undergo a low number of full or partial wavelength shifts (also referred to as the order, or m) in addition to the fractional design retardance. This differs from true zero-order and multi-order wave plates which undergo no shift or a high number of shifts, respectively. The low-order design maintains near to true zero-order performance, making it a good alternative to true zero-order wave plates. The single magnesium fluoride substrate is also thinner compared to a zero-order design, which combines two multi-order wave plates, making our low-order retarders well suited for applications that are sensitive to dispersion.
Multi-Order Wave Plates are made such that the retardance of a light path will undergo a certain number of full wavelength shifts (also referred to as the order, or m) in addition to the fractional design retardance. Compared to their zero-order counterparts, the retardance of multi-order wave plates is more sensitive to wavelength and temperature changes. Multi-order wave plates are, however, a more economical solution for many applications where increased sensitivities are not an issue. Our multi-order wave plates are available for a number of discrete wavelengths ranging from 405 nm to 1550 nm. Thorlabs also offers Dual-Wavelength Multi-Order Wave Plates designed for use at both 532 nm and 1064 nm.
In addition to these options, Thorlabs also has the ability to design and manufacture custom wave plates for both OEM sales and individual low quantity orders. Our technical staff is able to help with all phases of your request: quoting, sales, and planning and manufacturing support. If you have a custom request or a question about our capabilities, please contact Tech Support to start a discussion.
 Products Home
Products Home





 Click to Enlarge
Click to Enlarge


 Dual-Wavelength Wave Plates
Dual-Wavelength Wave Plates