12 W Laser Diode Temperature Controller

- Low Noise TEC Current: ±2 A
- Excellent Temperature Stability: ≤0.002 °C
- Separate P, I, and D-Gain Control
TED200C Front Panel (°C Display when Used with the AD590
Temperature Transducer, kΩ when Used with a Thermistor)
TED200C
CAB420-15

Please Wait
| Key Specifications | |
|---|---|
| Control Range | -2 A to 2 A |
| Compliance Voltage | >6 V |
| Maximum Output Power | 12 W |
| Control Range | 10 Ω to 20 kΩ / 100 Ω to 200 kΩ (2 Ranges) |
| Supported Sensors | AD590, AD592, LM135, LM335 |
Features
- Compatible Sensors: Thermistors, AD590/AD592, LM335
- TEC Output (Low Noise): ±2 A / 12 W
- Temperature Range from -45 °C to +145 °C (AD590) or 10 Ω to 200 kΩ (Thermistor)
- Temperature Resolution: 0.01 °C (IC-Sensor) or 1 Ω (Thermistor)
- Temperature Stability: ≤0.002 °C
- Separate Adjustment of the P, I and D Share of the Control Loop for Shortest Temperature Settling Time
- Constant Temperature Operating Mode
- Analog Control via the TUNE IN Input
- Adjustable TEC Current Limit
- Detection of Incorrect or Missing Temperature Sensor and Open TEC Connection
- RoHS Compliant
Applications
- Precise Stabilization of Laser Diodes for Use in Interferometry and Spectroscopy
- Cooling of Detectors for Noise Reduction
- Temperature Stabilization of Non-linear Crystals
- Temperature Stabilization of Industrial Systems
- Control Temperature Set Point via External Input for Active Stabilization of Laser Wavelength
Introduction
The TED200C is a precision temperature controller designed to drive thermoelectric cooler (TEC) elements with currents up to ±2 A. It supports almost all common temperature sensors and can be adapted to different thermal loads. A set of safeguard features and error indicators protects the connected TE coolers and laser diodes from damage. For an easy connection with external devices, or integration into control loops, the TED200C can be controlled via an analog voltage input and output. For higher currents, up to ±15 A, please see the TED4000 Temperature Controller Series.
Thorlabs recommends recalibrating these controllers every 24 months and offers a factory recalibration service. To order this service, scroll to the bottom of the page and select Item # CAL-TED2.
Note: The updated TED200C is now RoHS compliant. The rest of the features are virtually the same as the obsoleted product TED200.
Operation
The integrated 5-digit display of the TED200C shows the actual temperature reading, the set temperature, the heating or cooling current, or the current limit for the TE cooler. If used with a thermistor sensor, the TED200C will indicate the resistance (as opposed to the actual temperature); correlated temperatures can be calculated manually using the equation found in section 3.1.3.1 of the manual. The temperature set point can be controlled either by adjusting the large front panel control knob or via external signal input into the analog input connector at the rear of the controllers. The latter can be used in control loop mode for locking the wavelength of the laser diode by adjusting the temperature.
Adaptability to Different Thermal Loads
The TED200C can easily be adapted to different thermal loads using the PID feedback circuit that allows the user independent setting of the P (proportional) gain, the I (integral) offset control, and the D (derivative or differential) rate. The proportional gain optimizes the response time of the feedback loop, while the integral gain provides precise zero-offset regulation. The derivative gain optimizes the dynamic response of the feedback loop to accommodate rapid changes in the thermal load. With optimum PID adjustment the settling time is less than 2 seconds for a temperature change from 30 °C to 20 °C for a laser in a butterfly package mounted in our LM14S2 laser diode mount (using a butterfly package with integrated thermistor). The PID controls are located on the front panel for easy access when optimizing the response of the controller.
Supported Temperature Sensors
The TED200C Temperature Controller supports most common temperature sensors. A sensor selection switch allows the use of thermistors up to 200 kΩ or a temperature sensing IC (AD590, AD592, and LM335).
When a thermistor is selected, the temperature is displayed as the resistance value of the thermistor. When an AD590, AD592, or an LM335 is selected, the temperature is displayed in degrees Celsius, with a temperature set range of -45 °C to +145 °C. The actual control range is limited by the temperature rating of the connected IC sensor.
TEC Protection Features
The TED200C is designed for maximum TEC element protection. The limit adjustment of the TEC output current prevents the controller from overdriving the TEC element. This limit can be set anywhere within the current range of the controller.
Error Indication
The system indicates the presence of an incorrect or missing temperature sensor, or a bad connection between sensor and controller by an error LED together with an acoustic warning signal, and the TEC current is automatically switched off.
Temperature Monitor Output
For monitoring purposes, the TED200C provides an output voltage signal that is proportional to the actual temperature being measured. The signal is accessed via a BNC connector located on the back panel. This feature allows long term temperature recording of a device.
Companion Products
The LDC200 Laser Diode Controller Series is an ideal companion for the TED200C. When combined with our TEC laser mounts, the TED200C can achieve a thermal stability of 1 mK, robust enough for applications like diode laser wavelength tuning and atomic absorption cell spectroscopy.
Connection Cables
A CAB420-15 is required to connect the TED200C to a Thorlabs' Laser Diode Mount. One cable is included with the TED200C, it has a length of 1.5 m. Additional cables can be ordered below.
| TED200C Specifications | |
|---|---|
| TEC Current Output | |
| Control Range | -2 A to 2 A |
| Compliance Voltage | >6 V |
| Maximum Output Power | 12 W |
| Measurement Resolution | 1 mA |
| Accuracy | ±10 mA |
| Noise and Ripple (Typ.) | <1 mA |
| TEC Current Limit | |
| Setting Range | 0 to >2 A |
| Measurement Resolution | 1 mA |
| Accuracy | ±20 mA |
| Thermistor Sensorsa | |
| Control Range | 10 Ω to 20 kΩ / 100 Ω to 200 kΩ (2 Ranges) |
| Setting Resolution (20 kΩ / 200 kΩ Range) |
1 Ω / 10 Ω |
| Measurement Resolution (20 kΩ / 200 kΩ Range) |
1 Ω / 10 Ω |
| Accuracy (20 kΩ / 200 kΩ Range) | ±10 Ω / ±100 Ω |
| Temperature Stability (24 Hours)b (20 kΩ / 200 kΩ Range) |
<0.5 Ω / <5 Ω |
| IC Sensors | |
| Supported Sensors | AD590, AD592, LM135, LM335 |
| Control Range with AD590, LM135 | -45 °C to 145 °C |
| Control Range with AD592 | -25 °C to 105 °C |
| Control Range with LM335 | -40 °C to 100 °C |
| Setting Resolution | 0.01 °C |
| Measurement Resolution | 0.01 °C |
| Accuracy (Except LM335) | ±0.1 °C |
| Temperature Stability (24 Hours) | <0.002 °C |
| Temperature Control Input | |
| Input Resistance | 10 kΩ |
| Control Voltage | -10 V to +10 V |
| Transmission Coefficient Thermistor (20 kΩ / 200 kΩ Range) |
2 kΩ/V / 20 kΩ/V ± 5% |
| Transmission Coefficient IC-Sensors |
20°C/V ± 5% |
| Temperature Control Output | |
| Load Resistance | >10 kΩ |
| Transmission Coefficient Thermistor (20 kΩ / 200 kΩ Range) |
500 mV/kΩ / 50 mV/kΩ ± 5% |
| Transmission Coefficient IC-Sensors |
50 mV/°C ± 5% |
| General Data | |
| Safety Features | TEC Current Limit, Short Circuit When TEC Off, No Sensor Protection, Open Circuit Detection, Over Temperature Protection |
| Display | LED, 5 Digits |
| Connector for Sensor, TE Cooler, TEC On Signal | 15-Pin D-Sub Jack |
| Connectors for Control Input / Output | BNC |
| Chassis Ground Connector | 4 mm Banana Jack |
| Line Voltage | 100 V, 115 V, 230 V +15%/-10% Each |
| Line Frequency | 50 to 60 Hz |
| Maximum Power Consumption | 60 W |
| Mains Supply Overvoltage | Category II (Cat II) |
| Operating Temperature | 0 to 40 °C |
| Storage Temperature | -40 to 70 °C |
| Relative Humidity | Max. 80% Up to 31 °C, Decreasing to 50% at 40 °C |
| Pollution Degree (Indoor Use Only) | 2 |
| Operation Altitude | <2000 m |
| Warm-up Time for Rated Accuracy | 10 min |
| Weight | <3.1 kg |
| Dimensions (W x H x D) without Operating Elements | 146 mm x 66 mm x 290 mm |
| Dimensions (W x H x D) with Operating Elements | 146 mm x 77 mm x 320 mm |
All technical data valid at 23 ± 5 °C and 45 ± 15% relative humidity.
TED200C Front Panel
| Callout | Connection | Callout | Connection |
|---|---|---|---|
| 1 | 5-Digit LED Display | 8 | Display Indicators |
| 2 | Display Units | 9 | Up/Down Display Select |
| 3 | Interlock Indicators | 10 | Selected Sensor Inticators |
| 4 | TEC Status Indicator | 11 | Sensor Select Key |
| 5 | TEC Current On/Off Switch | 12 | Potentiometers for PID Gain Settings |
| 6 | Supply Power Switch | ||
| 7 | Potentiometer for Current Limit Setting | 13 | Display Adjustment Knob |
TED200C Back Panel
| Callout | Connection | Callout | Connection |
|---|---|---|---|
| 1 | Analog Temperature Control Input "Tune In", -10 to 10 V | 5 | 15-pin D-sub Jack for the TEC Element and the Temperature Sensor "TE OUTPUT" |
| 2 | Analog Temperature Control Output "CTL Out", -10 to 10 V | 6 | Serial Number of the Unit |
| 3 | Cooling Fan | 7 | Indicator / Switch for Line Voltage (Included in Fuse Holder) |
| 4 | 4 mm Banana Jack for Chassis Ground | 8 | Power Connector and Fuse Holder |
| Pin | Connection | Pin | Connection |
|---|---|---|---|
| 1 | Status LED (+) TEC ON/OFF | 9 | Not Connected |
| 2 | Not Connected | 10 | Transducer AD 590/592 (-), LM 135/335 (+) |
| 3 | Thermistor (-), Ground | 11 | Transducer AD 590/592 (+), LM 135/335 (+) |
| 4 | Thermistor (+) | ||
| 5 | TEC (+) | 12 | Not Connected |
| 6 | TEC (+) | 13 | TEC (-) |
| 7 | TEC (+) | 14 | TEC (-) |
| 8 | AGND LM 135/335 (-), Status LED (-) | 15 | TEC (-) |
Temperature Sensor and Controllera
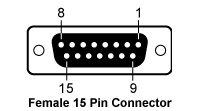
Analog Temperature Control Input

-10 ... 10 V
Analog Temperature Control Output
-10 ... 10 V
Chassis Ground

| TED200C | Part |
|---|---|
| x | Benchtop Temperature Controller, ±2A/12 W (TED200C) |
| x | Cable for Temperature Controller with 15-pin D-Sub Connector (CAB420-15) |
| x | Operating Manual TED200C |
| x | Power Cord |
PID Basics
The PID circuit is often utilized as a control loop feedback controller and is commonly used for many forms of servo circuits. The letters making up the acronym PID correspond to Proportional (P), Integral (I), and Derivative (D), which represents the three control settings of a PID circuit. The purpose of any servo circuit is to hold the system at a predetermined value (set point) for long periods of time. The PID circuit actively controls the system so as to hold it at the set point by generating an error signal that is essentially the difference between the set point and the current value. The three controls relate to the time-dependent error signal. At its simplest, this can be thought of as follows: Proportional is dependent upon the present error, Integral is dependent upon the accumulation of past error, and Derivative is the prediction of future error. The results of each of the controls are then fed into a weighted sum, which then adjusts the output of the circuit, u(t). This output is fed into a control device, its value is fed back into the circuit, and the process is allowed to actively stabilize the circuit’s output to reach and hold at the set point value. The block diagram below illustrates the action of a PID circuit. One or more of the controls can be utilized in any servo circuit depending on system demand and requirement (i.e., P, I, PI, PD, or PID).
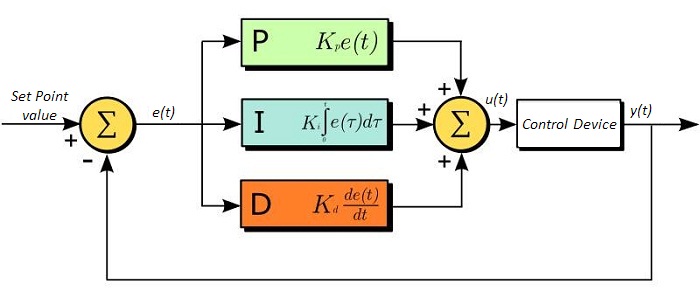
Through proper setting of the controls in a PID circuit, relatively quick response with minimal overshoot (passing the set point value) and ringing (oscillation about the set point value) can be achieved. Let’s take as an example a temperature servo, such as that for temperature stabilization of a laser diode. The PID circuit will ultimately servo the current to a Thermo Electric Cooler (TEC) (often times through control of the gate voltage on an FET). Under this example, the current is referred to as the Manipulated Variable (MV). A thermistor is used to monitor the temperature of the laser diode, and the voltage over the thermistor is used as the Process Variable (PV). The Set Point (SP) voltage is set to correspond to the desired temperature. The error signal, e(t), is then the difference between the SP and PV. A PID controller will generate the error signal and then change the MV to reach the desired result. For example, if e(t) states that the laser diode is too hot, the circuit will allow more current to flow through the TEC (proportional control). Since proportional control is proportional to e(t), it may not cool the laser diode quickly enough. In that event, the circuit will further increase the amount of current through the TEC (integral control) by looking at the previous errors and adjusting the output to reach the desired value. As the SP is reached (e(t) approaches zero), the circuit will decrease the current through the TEC in anticipation of reaching the SP (derivative control).
Please note that a PID circuit will not guarantee optimal control. Improper setting of the PID controls can cause the circuit to oscillate significantly and lead to instability in control. It is up to the user to properly adjust the PID gains to ensure proper performance.
PID Theory
The output of the PID control circuit, u(t), is given as
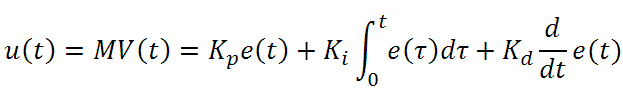
where
Kp= Proportional Gain
Ki = Integral Gain
Kd = Derivative Gain
e(t) = SP - PV(t)
From here we can define the control units through their mathematical definition and discuss each in a little more detail. Proportional control is proportional to the error signal; as such, it is a direct response to the error signal generated by the circuit:
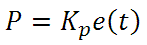
Larger proportional gain results in larger changes in response to the error, and thus affects the speed at which the controller can respond to changes in the system. While a high proportional gain can cause a circuit to respond swiftly, too high a value can cause oscillations about the SP value. Too low a value and the circuit cannot efficiently respond to changes in the system.
Integral control goes a step further than proportional gain, as it is proportional to not just the magnitude of the error signal but also the duration of the error.
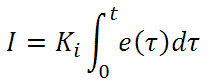
Integral control is highly effective at increasing the response time of a circuit along with eliminating the steady-state error associated with purely proportional control. In essence integral control sums over the previous error, which was not corrected, and then multiplies that error by Ki to produce the integral response. Thus, for even small sustained error, a large aggregated integral response can be realized. However, due to the fast response of integral control, high gain values can cause significant overshoot of the SP value and lead to oscillation and instability. Too low, and the circuit will be significantly slower in responding to changes in the system.
Derivative control attempts to reduce the overshoot and ringing potential from proportional and integral control. It determines how quickly the circuit is changing over time (by looking at the derivative of the error signal) and multiplies it by Kd to produce the derivative response.
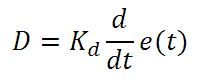
Unlike proportional and integral control, derivative control will slow the response of the circuit. In doing so, it is able to partially compensate for the overshoot as well as damp out any oscillations caused by integral and proportional control. High gain values cause the circuit to respond very slowly and can leave one susceptible to noise and high frequency oscillation (as the circuit becomes too slow to respond quickly). Too low and the circuit is prone to overshooting the SP value. However, in some cases overshooting the SP value by any significant amount must be avoided and thus a higher derivative gain (along with lower proportional gain) can be used. The chart below explains the effects of increasing the gain of any one of the parameters independently.
| Parameter Increased | Rise Time | Overshoot | Settling Time | Steady-State Error | Stability |
|---|---|---|---|---|---|
| Kp | Decrease | Increase | Small Change | Decrease | Degrade |
| Ki | Decrease | Increase | Increase | Decrease Significantly | Degrade |
| Kd | Minor Decrease | Minor Decrease | Minor Decrease | No Effect | Improve (for small Kd) |
Tuning
In general the gains of P, I, and D will need to be adjusted by the user in order to best servo the system. While there is not a static set of rules for what the values should be for any specific system, following the general procedures should help in tuning a circuit to match one’s system and environment. A PID circuit will typically overshoot the SP value slightly and then quickly damp out to reach the SP value.
Manual tuning of the gain settings is the simplest method for setting the PID controls. However, this procedure is done actively (the PID controller turned on and properly attached to the system) and requires some amount of experience to fully integrate. To tune your PID controller manually, first the integral and derivative gains are set to zero. Increase the proportional gain until you observe oscillation in the output. Your proportional gain should then be set to roughly half this value. After the proportional gain is set, increase the integral gain until any offset is corrected for on a time scale appropriate for your system. If you increase this gain too much, you will observe significant overshoot of the SP value and instability in the circuit. Once the integral gain is set, the derivative gain can then be increased. Derivative gain will reduce overshoot and damp the system quickly to the SP value. If you increase the derivative gain too much, you will see large overshoot (due to the circuit being too slow to respond). By playing with the gain settings, you can maximize the performance of your PID circuit, resulting in a circuit that quickly responds to changes in the system and effectively damps out oscillation about the SP value.
| Control Type | Kp | Ki | Kd |
|---|---|---|---|
| P | 0.50 Ku | - | - |
| PI | 0.45 Ku | 1.2 Kp/Pu | - |
| PID | 0.60 Ku | 2 Kp/Pu | KpPu/8 |
While manual tuning can be very effective at setting a PID circuit for your specific system, it does require some amount of experience and understanding of PID circuits and response. The Ziegler-Nichols method for PID tuning offers a bit more structured guide to setting PID values. Again, you’ll want to set the integral and derivative gain to zero. Increase the proportional gain until the circuit starts to oscillate. We will call this gain level Ku. The oscillation will have a period of Pu. Gains for various control circuits are then given below in the chart.
| Posted Comments: | |
昊阳 Du
(posted 2023-06-06 17:01:51.237) 您好,我们有意向购买一台TED200C温度控制器,但其中有些问题还需要进一步咨询。 cdolbashian
(posted 2023-06-12 11:02:09.0) 感谢联系Thorlabs!我们的技术支持团队将会直接联系您,以便与您进一步讨论。
Thank you for contacting Thorlabs! Our Tech Support Team will reach out to you directly for further discussion. user
(posted 2023-05-23 15:38:14.183) If is it possible to use TED200C with resistive heater (not TEC) or due to the polarity change the cooling will not take place? Thanks in advance wskopalik
(posted 2023-05-25 08:49:28.0) Thank you for your feedback!
The TED200C is designed for TEC elements only. The temperature control loop expects the element to cool in one polarity and heat in the other. Resistive heater will however heat in both polarities. So in some conditions the loop could become unstable when a heater is used instead of a TEC element.
For resistive heaters we e.g. offer the heater temperature controller TC300. user
(posted 2023-05-09 09:58:15.503) The current range to drive the TEC200C is noted as 2A. I would need to change the temperature a bit more and need more current: what is the maximum current output that does not risk any damage to the device? hchow
(posted 2023-05-10 07:40:37.0) Dear User, thank you for your feedback. The maximum current that can be set on the TED200C is 2 Amperes. You can do this by using a flat head screw driver and turning 12-turn potentiometer to its highest setting. The adjustable potentiometer is found just beside the word LIM I under the Display box on the lower part of the front face of the TED200C. isaac Schmidt
(posted 2021-11-14 10:32:13.937) Hello
I have a TEC12706. can i use TED200C to control it?
regards soswald
(posted 2021-11-15 04:33:38.0) Dear Isaac,
thank you for your feedback.
The TEC12706 requires 65 W, 15 V and 6.4 A.
The TED200C delivers up to 12 W, 6 V and 2 A, so it is not suitable to drive this particular TEC.
We recommend TED4015 for this TEC. Hangbo Shi
(posted 2021-10-25 10:48:26.333) Will there be a replacement for the TC200? When will the replacement be available? YLohia
(posted 2021-12-23 10:44:42.0) Thank you for contacting Thorlabs. We are working on a replacement (TC300) and it is expected to be added to our catalog in Q1 2022. Héctor Álvarez Martínez
(posted 2021-09-30 08:46:15.167) 1/ I will use to temperature-control a doubling crystal which has 2 pins for a temperature cooler and other 2 pins for a thermistor. In the specs the manufacturer only gives the TEC current (2 A max, which is fine) and the B parameter = 3450 (nothing about the temperature range and a reference resistor value). That would be enough? Do I need more specs regarding the thermistor?
2/ Can the TED200C control both the thermistor and the temperature cooler?
3/ Would I have to do any adjustment with the thermal load? soswald
(posted 2021-10-05 04:41:23.0) Dear Héctor,
since more details about your thermistor and thermal load are required, I have reached out to you directly for further discussions. Petar Bojovic
(posted 2020-09-24 10:33:14.037) Dear Thorlabs,
we are happily using many of your temperature and current controllers and I am writing you with the suggestion how to slightly improve them.
In our case, the big tuning knobs can be quite annoying because they turn too easily. For example, when we are touching some electronics above the optical table even the lightest touch with the sleeve would turn the knob and change the current or the set temperature of the laser - often resulting in an unlocked laser. Or when we are tuning the D parameter on temperature controller we always unintentionally change the set temperature (because the knobs are so close).
We've solved the problem by gluing the plastic tube around the knobs, but there are plenty of elegant and smart solutions. I hope you will consider fixing this "knob problem" in your future designs. :)
Thank you and best regards,
Petar Bojovic MKiess
(posted 2020-09-25 07:32:46.0) Dear Petar, thank you very much for this feedback. We are always looking forward to your suggestions to improve our products and make them better. Such feedback helps us significantly to realize this. Thanks a lot for your feedback. jhenhan99
(posted 2018-09-12 15:54:24.577) Dear supporter, I'm hoping to use the I share of PID control to stabilize the temperature, but I found that even the lowest level of I share is too much for my laser. Is there any way to get I values below the minimum? wskopalik
(posted 2018-09-18 03:06:40.0) This is a response from Wolfgang at Thorlabs. Thank you very much for your inquiry!
Unfortunately, it isn't possible to decrease the I share even further on the TED200C if the potentiometer is already in the lowest position. You could only switch the I share off completely.
Usually it is best to use the P, I and D share together to stabilize the temperature to a constant level. There are instructions in the manual how to find the best settings for a particular setup and I will contact you directly to provide further assistance. cihadgltkn
(posted 2018-01-29 08:58:59.897) Dear supporter,
your product TED200C show that "no sensor"
could you please share some way to solve the problem?
best regards
Cihad wskopalik
(posted 2018-01-29 10:09:03.0) This is a response from Wolfgang at Thorlabs. Thank you very much for your inquiry!
The "NO SENSOR" LED indicates that either no temperature sensor or an incompatible temperature sensor is connected. The TED200C supports thermistors between 10 Ohm - 200kOhm and IC sensors of type AD590, AD592, LM335.
I will contact you directly so we can discuss the issue in more detail. francois.mondain
(posted 2018-01-03 16:08:35.77) Dear Sir/Madam
For us it is really important to remove the integrate share of the PID loop. I read that we can do it by pressing the key f25. In this way, is it physically removed, or just "software" removed?
Is there any jumper, wire, that we can disconnect to be sure that there is no integrated share anymore? wskopalik
(posted 2018-01-08 08:11:51.0) This is a response from Wolfgang at Thorlabs. Thank you very much for your inquiry!
The procedure described in the manual (i.e. pressing the button "F25" for more than 1 second) is the only way to disable the integral I share of the PID loop completely. This function disables the circuitry responsible for the I share on the control board, so it is not a software function.
In comparison turning the I share potentiometer ("F23") to the lowest position would still leave the I share enabled at a low level.
I will contact you directly with more detailed information. nzhang
(posted 2016-08-03 19:34:00.673) Dear Sir/Madam,
I'm interested in your product TED200C. Could you tell me whether this product can be applied to a process control, instead of temperature control. I noticed that there are PID loop in TED200C, so can this PID loop be used in other control systems rather than temperature control.
Thank you.
Best regards swick
(posted 2016-08-03 08:30:41.0) This is a response from Sebastian at Thorlabs.
Thank you very much for contacting us. I have contacted you directly to discuss your application in detail. tbeom
(posted 2013-11-11 11:09:34.477) we have an TED 200C. It was working satisfactory for long time. Suddenly I got an "err06" on display. Please let me know what is "err06" and how to fix it here without returning it. Thanks. Taebong. jlow
(posted 2013-11-11 10:52:36.0) Response from Jeremy at Thorlabs: The err06 means that the firmware needs to be updated. We will have to take the unit back to have the firmware updated. We will contact you on sending this back for the firmware update. labonte
(posted 2013-09-24 10:14:24.367) I am using TED200C with a transducer AD590 and a heater. I'm interested by exporting both the temperature Tact and the currnt Itec. I used the "CTL output" to control the Tact. Is it possible to export the current (i.e Itec) from the temperature controller to the heater which is displayed at the front panel ?
Many thanks.
Laurent tschalk
(posted 2013-09-24 12:04:00.0) This is a response from Thomas at Thorlabs. Thank you very much for your inquiry. Unfortunately there is no possibility to export the actual current value. Therefore you could use a TED4000-Series Controller which is equipped with an USB port. I will contact you directly with more detailed information. tschalk
(posted 2012-12-10 11:49:00.0) This is a response from Thomas at Thorlabs. Thank you very much for your inquiry. The LM14S2 does not contain any temperature sensor or TEC element. Those are normally integrated in the butterfly package. The temperature sensitivity of the integrated temperature sensor should be specified in the data sheet of the laser diode. I will contact you directly for more detailed information. Best Regards, Thomas bslalit
(posted 2012-12-10 01:17:53.377) I am using LM14S2 mount(for NEL laser diode NLK1S5GAAA) with TED200C controller. I am not able to select AD590 sensor as mentioned by apalmentieri below. Can you please send me resistance vs temperature curve for LM14S2. jlow
(posted 2012-07-31 14:59:00.0) A response from Jeremy at Thorlabs: The rate of heating/cooling can be found from the spec sheet for the TEC that is being used. For the TEC3-2.5, you can find the performance curve at http://www.thorlabs.com/Thorcat/4800/TEC3-2.5-SpecSheet.pdf, on page 2. The heat transfer rate would not be constant at constant current because of the temperature change. jvigroux
(posted 2012-07-30 06:08:00.0) A response from Julien at Thorlabs: ERR06 is an internal error message that indicates that the EEPROM within the TED200C could not be accessed. This type of error usually occurs when a hardware component is damaged. I would thus recommend returning the device for inspection. I will contact you directly to see how we could solve this problem as fast as possible. yinon
(posted 2012-07-30 10:27:47.0) we have an TED 200C temperature controler,working
satisfactory for long time.
Suddenly we received an "err06" on display.
After few days not working it recovered and look
ordinary.
Pls. advise what is "err06".
Thanks and rgds
Yinon Barak silviutpopescu
(posted 2012-07-25 03:55:24.0) Hi,
How can I find the rate of heating, temperature(time), at constant current (for example if I have current limit of 1A) . I'm using a TEC3-2.5 Peltier heater and a 20k Thermistor as a sensor. Is the rate of heating constant at constant current ? jjurado
(posted 2011-02-03 17:00:00.0) Response from Javier at Thorlabs to karl-alexandre.jahjah: Thank you very much for submitting your inquiry. Err.06 indicates that there is a problem in the EEPROM of the unit, which can caused by many different factors. In order to fix this, we need to upgrade the firmware of the controller. We will add this information to the TED200C manual. I will also contact you directly to set up the return authorization. karl-alexandre.jahjah.1
(posted 2011-02-03 14:56:06.0) Hi, I have been using the TED200C for over a year without any problems. Today, the TED200C displayed err.06. Nothing is said about this error code in the manual. What is going on? Please reply fast,
thanks in advance! julien
(posted 2010-04-23 17:57:22.0) a response form Julien at Thorlabs: The voltage compliance listed in the specs (6V) corresponds to an absolute voltage compliance. There is indeed a small variation of the compliance with the load but it is far from being sufficient to multiply the compliance by 6. This applies to both the TED200C and the TD350. I will contact you directly to see if another solution can be found to obtain the result you need. jean-michel.melkonian
(posted 2010-04-23 09:31:02.0) Hi,
What is the maximum compliance voltage of this controller for the TEC element, independently of the maximum power? In other words, is it possible to drive 6 TEC in series at 4*6=24V with 0.5A? I have the same question for the discontinued TD350 (40W).
Thank you. apalmentieri
(posted 2010-01-11 09:06:03.0) A response from Adam at Thorlabs to tswang: The sensors that are selectable depend on the mounts your are using to hold the photodiode. If you are using our TCLDM9, LDM21, or LM14S2 mounts then the AD590 sensor should be selectable. If you are not using these mounts, it may not be selectable. If you are using our TCLDM9, LDM21, or LM14S2 mounts, then the resistance, R(0), is 10KOhms +/- 3% and the temperature, T(0), is 298K. The Energy Constant, Bval, is 3977K +/- .75%. The TCLDM9 manual contains a temperature vs. Resistance curve, which can be found on page 10. I will send you a copy of the curve via email. tswang
(posted 2010-01-09 23:48:04.0) hi Thorlabs, A new TED200C just arrived at our FOL lab in CREOL of UCF. 1)I can not select the thermal sensor of "AD590" by pressing F25 key. Do I must pay extra money for the AD590 temperature sensor? 2)The formula describing the dependence of resistance on temperature is given in the operation manual. I need some of parameters, such as R_0(Thermistor nominal resistance at termperaure T_0) and B_val(Energy constant) to derive the temperature value reversely. Unfortunately, there is no the data sheet of the thermistor available. Please send me on copy. Thanks!(My name is Tian^_^) leichner
(posted 2009-10-20 17:07:23.0) A response from Lou at Thorlabs to pmorton: Our typical TEC controllers sense only the resistance (and its change) which is typically good enough for laser diode stabilization. These models do not have a uController to control the operation. Our higher end models have the ability to convert the thermistor values to degree. Our TED8xxx models can do (you can enter individual NTC parameters), ITC8xxx models as well, and the new TED4015 can do the same. All other models w/o a CPU (TED350, TED200) cannot. pmorton
(posted 2009-10-19 11:46:30.0) Why do your two temperature controllers (12W and 40W) not provide a temperature readout when using a thermistor sensor? Without that they are not very useful - I want to control and readout temperature not resistance. I would purchase one of the units if they did so!
Paul Laurie
(posted 2008-05-19 09:41:22.0) Response from Laurie at Thorlabs to Danny: Thank you for your feedback. When using the TED200C with thermistor sensor, the TED200C (by design) will indicate resitance as opposed to temperature. Correlated temperature can be calculated manually using the equation found in section 3.1.3.1 of the manual. Please note that in general, thermistor-specific data (such as R0, beta, or Steinhart-hart coefficients) cannot be recognized electronically. If you should have further questions, please do not hesitate to contact our technical support staff by dialing 973-300-3000 and asking to speak to an applications engineer. danny.shushan
(posted 2008-05-18 06:05:12.0) How does the TED200C, refer to different values of the thermistor beta ? ,how does the TED200C regocnize the spesific beta of my thermistor?
I intend to set a working temperature of my TEC to +70 deg C, can the TED200C do this with my thermistor 10kOhm:
"FH10-6Q103FC, beta(k)(25/50 deg C) = 3410" |

The pin descriptions shown in the first two tables below denote the typical pin assignments used by Thorlabs' family of laser diode temperature controllers and laser diode mounts. The third table gives the physical pin connections between the 15-pin and 9-pin sides of the CAB420-15 cable.
 |
|
| 1 | Status LED (+) (for TEC On/Off Indication)a |
| 2 | TEC Voltage Measurementb |
| 3 | Thermistor (-), Ground |
| 4 | Thermistor (+) |
| 5 | TEC (+) |
| 6 | TEC (+) |
| 7 | TEC (+) |
| 8 | LM 135/335 (-), Grounda |
| 9 | TEC Voltage Measurementb |
| 10 | Transducer AD 590/592 (-), LM 135/335 (+) |
| 11 | Transducer AD 590/592 (+), LM 135/335 (+) |
| 12 | No Connection |
| 13 | TEC (-), Status LED (-) |
| 14 | TEC (-), Status LED (-) |
| 15 | TEC (-), Status LED (-) |
 |
|
| 1 | Status LED (+) (for TEC On/Off Indication)a |
| 2 | Thermistor (+) |
| 3 | Thermistor (-), Ground |
| 4 | TEC (+) |
| 5 | TEC (-), Status LED (-) |
| 6 | No Connection |
| 7 | Transducer AD 590/592 (-), LM 135/335 (+) |
| 8 | LM 135/335 (-), Grounda |
| 9 | Transducer AD 590/592 (+), LM 135/335 (+) |
| Pin Connections | |
|---|---|
| 15-Pin Side | 9-Pin Side |
| 1 | 1 |
| 2 | 4 |
| 3 | 3 |
| 4 | 2 |
| 5 | 4 |
| 6 | 4 |
| 7 | No Connection |
| 8 | 8 |
| 9 | 5 |
| 10 | 7 |
| 11 | 9 |
| 12 | No Connection |
| 13 | 5 |
| 14 | 5 |
| 15 | No Connection |

Thorlabs offers a recalibration service for the TED200C Benchtop Temperature Controller. To ensure accurate measurements, we recommend recalibrating the devices every 24 months.
Requesting a Calibration
Thorlabs provides two options for requesting a calibration:
- Complete the Returns Material Authorization (RMA) form. When completing the RMA form, please enter your name, contact information, the Part #, and the Serial # of the item being returned for calibration; in the Reason for Return field, select "I would like an item to be calibrated." All other fields are optional. Once the form has been submitted, a member of our RMA team will reach out to provide an RMA Number, return instructions, and to verify billing and payment information.
- Enter the Part # and Serial # of the item that requires recalbration below and then Add to Cart. A member of our RMA team will reach out to coordinate return of the item for calibration. Should you have other items in your cart, note that the calibration request will be split off from your order for RMA processing.
Please Note: To ensure your item being returned for calibration is routed appropriately once it arrives at our facility, please do not ship it prior to being provided an RMA Number and return instructions by a member of our team.
 Products Home
Products Home










 Zoom
Zoom 12 W Temperature Controller
12 W Temperature Controller