Free-Space Electro-Optic Modulators

- High Performance Lithium Niobate Amplitude & Phase Modulators
- SMA RF Modulation Input Connector
- Broadband DC Coupled or High-Q Resonant
EO-AM-NR-C1
EO-PM-NR-C2
EO-GTH5M Application
EO-PMT
EO-GTH5M
OVERVIEW
Lithium Niobate Electro-Optic Modulators
Thorlabs' free-space, lithium niobate, electro-optic (EO) modulators combine our expertise with crystal optics and high-speed electronics. Our EO modulators use MgO-doped lithium niobate to enable operation at higher power and shorter wavelengths. The modulators have an SMA RF input and are directly compatible with our HVA200 High-Voltage Amplifier (see Driver and Accessories). We offer both amplitude and phase modulators in non-resonant DC-coupled versions as well as high-Q, resonant, AC-coupled models, with anti-reflective coatings designed for a broad range of operating wavelengths.
Click to Enlarge
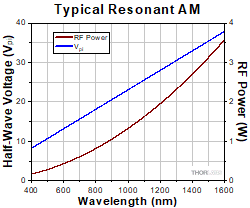
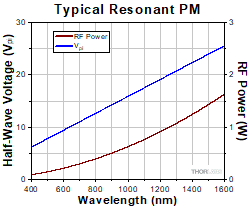
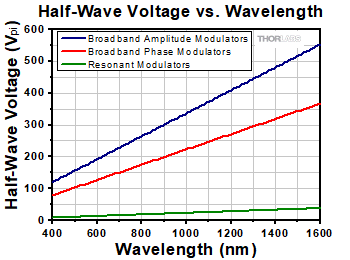
The required half-wave voltage needed to drive the EO modulators
is a function of the wavelength of the optical signal. The red and
blue lines correspond to the non-resonant EO Modulators while
the green line is for the resonant modulators. The half-wave voltage
shown for the resonant modulators is typical for the 20 MHz version.
Features
- High Performance in a Compact Package
- DC-Coupled, Non-Resonant or AC-Coupled, High-Q, Resonant
- 2 mm Diameter Clear Aperture
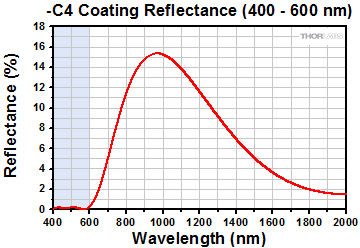
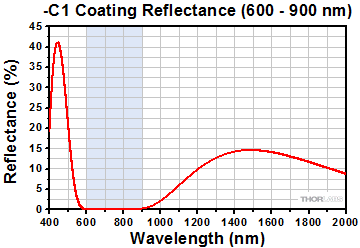
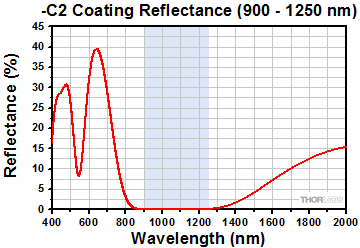
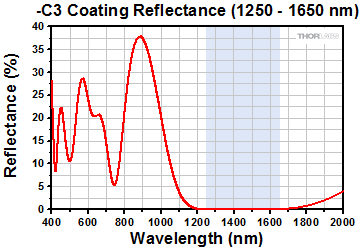
- Four Optical Bands: 400 - 600 nm, 600 - 900 nm, 900 - 1250 nm, and 1250 - 1650 nm
- MgO-Doped Lithium Niobate Crystals
- SMA RF Modulation Input Connector
- DC to 100 MHz Non-Resonant Bandwidth
- 20 MHz Standard Resonant Model
- Custom Resonant Frequencies from 0.1 - 100 MHz Available Upon Request
*Please note that modulators operating in the
400 - 600 nm range (C4 band) should only be used for AC modulation above a few Hz. MgO-doped lithium niobate can be sensitive to light in this wavelength range, displaying a slow negation to an applied DC field. The more intense the light, the faster the DC field is cancelled. Hence, in practice, a DC voltage cannot be used to bias the modulator at the desired operating point. Operation in the C4 band is also more sensitive to optical damage, so it is important to avoid excessive power density that can permanently damage the crystals.
DC-Coupled Non-Resonant Modulators
Our non-resonant EO modulators consist of EO crystals packaged in a rugged housing that is optimized for operation at any frequency from DC to
100 MHz. The user must supply an external high-voltage driver connected to the SMA RF input to achieve the desired modulation. The HVA200 driver can be used for frequencies up to 1 MHz. Please see the Specs tab for amplifier requirements. We offer amplitude and phase modulators with a
High-Q Resonant Modulators
Thorlabs' resonant EO Modulators operate at a much lower drive voltage, but at a fixed frequency using the built-in high-Q resonant circuit. Our standard resonant amplitude and phase modulators have a -C1 (600 - 900 nm) AR coating and operate at 20 MHz with a Q of about 15. Note that the Q at other, custom, resonant frequencies can be quite different. See the Graphs tab for more information on the coating reflectance. Standard and custom resonant frequencies are available from 0.1 to 100 MHz. Please contact
Driver and Accessories
Driving these non-resonant, free-space modulators can sometimes be challenging because the load is almost purely capacitive. Our HVA200 high-voltage amplifier, which features a low-noise, ±200 V output and
1 MHz bandwidth, is designed for driving these non-resonant EO modulators up to certain limits. The 400 V output swing allows the HVA200 to fully modulate our non-resonant amplitude modulators for wavelengths up to ~1200 nm and our non-resonant phase modulators across all wavelengths. The HVA200 also provides an adjustable DC bias to allow for electrical biasing to the quadrature operating point of an amplitude modulator, and effectively utilize the ±200 V bipolar output swing to achieve full modulation.
For driving these same non-resonant modulators at frequencies higher than 1 MHz, or at longer wavelengths with higher voltage, specialized amplifiers with sufficient output power, linearity, and bandwidth to drive capacitive loads are required. These modulators do not behave like a standard 50 Ω load. Please contact Tech Support for more information.
The resonant modulators, on the other hand, have a resonant circuit that is tuned to be a 50 Ω load at the resonant frequency. This means they can be driven at lower voltages with standard frequency generators designed for 50 Ω impedance. Note that the generator must be tuned to the exact same frequency the modulator is designed for. Thorlabs can customize resonant modulators to operate at any frequency between 0.1 and 100 MHz. However, the Q value is a function of the resonant frequency and may differ considerably compared to the 20 MHz models. Please contact Tech Support for details.
Thorlabs also offers a Glan-Thompson Polarizer mounting adapter, as well as an EO modulator mount for integration into our FiberBench collimation hardware (see below).
SPECS
Modulators
| Item # | EO Amplitude Modulator EO-AM-NR-Cx |
EO Phase Modulator EO-PM-NR-Cx |
EO Resonant Modulator EO-AM-R-20-C1 |
EO Resonant Modulator EO-PM-R-20-C1 |
|
|---|---|---|---|---|---|
| Modulator Crystal | Lithium Niobate (LiNbO3) Doped with MgO | ||||
| Wavelength Range | -C4 | 400 to 600 nma | N/Ab | ||
| -C1 | 600 to 900 nm | ||||
| -C2 | 900 to 1250 nm | N/Ab | |||
| -C3 | 1250 to 1650 nm | N/Ab | |||
| Clear Aperture | 2 mm Diameter | ||||
| Input Connector | SMA Female | ||||
| Operation Frequency | Broadband | 20 MHzc | |||
| Half Wave Voltage, Vpi (Click for Plot) | 205 V at 633 nm (Typical) (Click for Graph) |
136 V at 633 nm (Typical) (Click for Graph) |
15 V at 633 nmd (Typical) (Click for Graph) |
10 V at 633 nmd (Typical) (Click for Graph) |
|
| Extinction Ratio | >10 dB | N/A | >10 dB | ||
| Input Capacitance/Impedance | 14 pF | 50 Ohms | |||
| Max RF Input Power | N/A | 3 W (35 Vpp) | |||
| Max Optical Power Density | 2 W/mm2 @ 532 nm, 4 W/mm2 @ 1064 nm |
||||
GRAPHS
These plots show the reflectance of each of our four dielectric coatings for a typical coating run. The shaded region in each graph denotes the spectral range over which the coating is highly transmissive.
EO MODULATOR INTRO
Introduction to Electro-Optic Modulators
- Introduction
- Static Phase Retardance (SPR)
- EO Phase Modulator
- EO Polarization Modulator
- EO Amplitude Modulator
- Effect of SPR in Amplitude Modulators
- Amplitude Modulator Compensation
- Compensation Methods
- Temperature-Independent Amplitude Modulator
- Operation in the Thorlabs Housing
- Driving EO Modulators
Click for Details
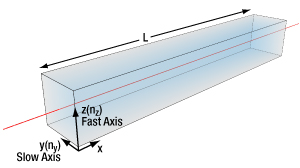
Figure 1: A schematic of a typical X-cut LN crystal used for EO modulators is displayed.
Introduction
Thorlabs' free-space electro-optic (EO) modulators enable users to modulate free-space optical beams at speeds up to 100 MHz. They are based on MgO-doped lithium niobate (LN), which is known for its efficient EO response and utility over a broad range of wavelengths. LN is a birefringent, uniaxial EO crystal typically used in the geometry depicted in Figure 1. The crystal is cut, with respect to the crystalline axes, for optical propagation along the x-axis with a driving voltage applied across the z-axis. This gives the highest EO response for both phase and amplitude modulators. In the following text, we describe the basic principles involved and how they lead to use of this crystal in phase, polarization, and amplitude modulators.
The crucial aspect of this crystal geometry is that light is only allowed to propagate with two orthogonal linear polarizations along the crystal’s y-axis and z-axis. Since the crystal is birefringent, the two polarizations will experience different optical indices, ny and nz , and will therefore travel at different speeds. The difference between the indices, (ny - nz), is denoted by Δn. For LN, ny is greater than nz , so light polarized along the y-axis (slow axis) travels slower than along the z-axis (fast axis). As a result, when light enters the crystal the two orthogonal linear polarizations will travel at different speeds and exit the crystal with a phase difference corresponding to the optical path difference, which is Δn times the crystal length, L.
Static Phase Retardance (SPR)
The phase difference resulting from the crystal’s inherent Δn is commonly known as the static phase retardance, and is represented here as SPR. The SPR is a function of Δn, the wavelength, λ, and crystal length, L. The factor of 2pi gives the SPR in radians while the factor of 360, in the alternate equation, provides it in degrees.
SPR (radians) = 2pi ⋅ Δn ⋅ L / λ or SPR (degrees) = 360 ⋅ Δn ⋅ L / λ
Since LN is an electro-optic material, applying a voltage along the crystal’s z-axis electrically modulates ny and nz , such that Δn becomes a function of voltage, enabling phase and amplitude modulators. We will see that the SPR does not affect phase modulator operation but can have significant consequences in the operation of amplitude modulators. The SPR is subject to environmental influences and variations in the crystal and EO module manufacturing process. The SPR is therefore module specific and, for certain applications, must be determined and compensated for because it can range anywhere from 0 to 2pi.*
*Note: When we refer to the phase retardance of orthogonal polarizations exiting the crystal, this also includes the majority of cases where the crystal is long and the phase retardance can be many multiples of 2pi. However, for a single wavelength of operation, it is only the “net” phase retardance between 0 and 2pi that actually matters.
Click to Enlarge
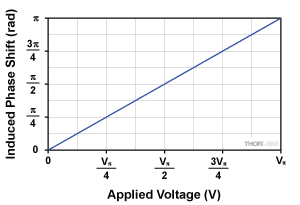
Figure 2b: Modulated Output Phase Response of a PM
Click to Enlarge
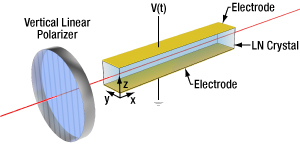
Figure 2a: Schematic of the Phase Modulator Configuration
EO Phase Modulator
The most efficient LN phase modulators (PMs) use input light that is vertically polarized along the same crystal axis as the applied voltage (z-axis), as shown in Figure 2a. Because the light is linearly polarized along only one of the principal birefringent axes, the SPR does not play a role, and the output polarization remains vertically polarized. In many applications, the absolute phase delay resulting from propagation at the output of the modulator is irrelevant. Only the modulated phase shift due to an applied voltage matters.
The applied modulation voltage, V(t), modulates nz , changing the optical path length and hence the phase shift of the output light. The half-wave voltage, known as Vpi, denotes the modulation voltage required to induce a pi (180°) phase shift. Figure 2b shows the voltage-induced phase shift due to the applied V(t). Here one can see that the resultant phase shift of the output light is linearly proportional to the applied voltage. The actual value of Vpi is a function of many factors (e.g. crystal dimensions and wavelength of light). For standard Thorlabs PMs, Vpi at 633 nm is about 150 V.
Click to Enlarge
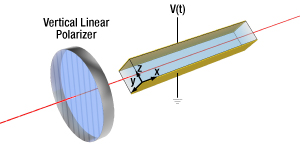
Figure 3: Schematic of the Polarization Modulator Configuration
EO Polarization Modulator
In an amplitude modulator (AM), the crystal is rotated 45° with respect to the modulator housing, while the input polarizer remains vertically oriented. Figure 3 illustrates this configuration. This results in the input light being equally split into two linear polarizations along the crystal y-axis and z-axis. These two components then develop a phase difference as they propagate through the crystal. This is the same principle as the SPR that was introduced earlier. We will now see that an applied voltage can introduce additional phase retardance, which we will call the voltage-induced phase retardance (VPR).
The applied voltage, V(t), changes the refractive indices along both the y-axis and z-axis, which introduces additional change to the phase retardance of the crystal. This additional voltage-induced phase retardance is called the VPR, which contributes to the total phase retardance (TPR) as given by:
TPR = SPR + VPR
It is the TPR that now determines the net phase retardance of the crystal. For example, in this case, when the TPR equals pi, the crystal behaves like a half-wave plate, resulting in a horizontal linear output polarization. A TPR of pi/2 would convert the linearly polarized input into a circularly polarized output, like a quarter-wave plate. Other phase differences yield various elliptical polarization states. In this way, the LN crystal rotated at 45° functions as a polarization modulator, as shown for a few standard cases in Figure 4.

Click to Enlarge
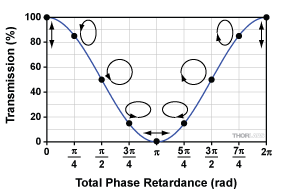
Figure 4: Above is the relationship between the output polarization state and the total phase retardance imparted by the crystal, assuming the input polarization is vertical.
Click to Enlarge
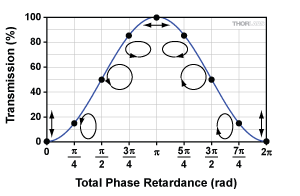
Figure 5b: Ideal Amplitude Modulator Transmission Function with Parallel Polarizers
Click to Enlarge
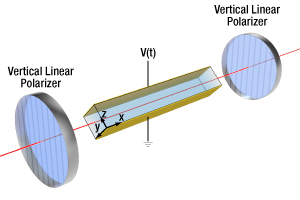
Figure 5a: Schematic of the Amplitude Modulator Configuration with Parallel Polarizers
Click to Enlarge
Figure 6b: Ideal Amplitude Modulator Transmission Function with Crossed Polarizers
Click to Enlarge
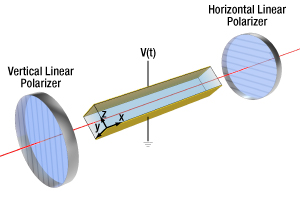
Figure 6a: Schematic of the Amplitude Modulator Configuration with Crossed Polarizers
EO Amplitude Modulator
To create an amplitude modulator, a linear polarizer is placed at the crystal output to convert polarization change into amplitude change. Figure 5a depicts one configuration, where the second polarizer is oriented parallel to the first. The fraction of light transmitted through the output polarizer depends on the polarization of the light exiting the crystal. Only the polarization component aligned with the polarizer is transmitted. The transmission function, as shown in Figure 5b, is given by:
T = cos2(TPR/2)
where, as in the previous section, TPR = SPR + VPR.
For amplitude modulators, Vpi refers to the voltage required to induce a VPR of pi (or 180°). If the TPR = 0, then polarization does not change from input to output, and the output polarizer permits maximum transmission. When TPR = pi, the output polarization changes to horizontal, giving minimum transmission through the vertical polarizer. If the TPR is further adjusted to equal 2pi (or 360°), the transmission is once again maximized. It is important to note the cos2 transmission function is periodic, so the transmission is the same for all multiples of 2pi.
Note that if the output polarizer is changed to horizontal (or more generally, crossed relative to the input polarizer), as shown in Figure 6a, then the curve in Figure 5b would shift along the horizontal axis by pi. This results in the transmission function shown in Figure 6b, where maximum transmission is now at a TPR = pi.
Click to Enlarge
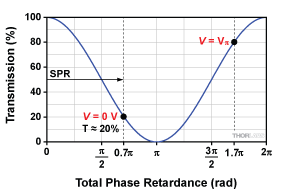
Figure 7: The above graph shows the effect of an arbitrary SPR on the voltage transmission response.
Effect of SPR in Amplitude Modulators
In practice, due to the unpredictable value of the SPR (which can be anything between 0 and 2pi), the transmission maximum likely does not occur at V = 0 V. SPR is a function of many factors like wavelength, temperature, and precise crystal dimensions. Out of the box, your EO modulator will probably have a nonzero SPR, meaning the transmission may take any value from 0 to 100% when V = 0 V (neglecting any losses from reflection and absorption).
The transmission curve in Figure 7 shows the effect of the SPR. For the sake of this example, we set the SPR at an arbitrary 0.7pi, but note that your modulator’s SPR can be anywhere between 0 and 2pi. In this example, the 0.7pi SPR sets the operating point (V = 0 V) transmission at ≈20%. Consequently, an applied voltage of Vpi would add an additional pi of VPR and thus give ≈80% relative transmission. Given the 0.7pi SPR in this example, you would have to add a voltage that induces an additional VPR of 0.3pi to reach the first transmission minimum. Or if you wanted to reach the maximum transmission, you would have to add a voltage that induces an additional 1.3pi of VPR.
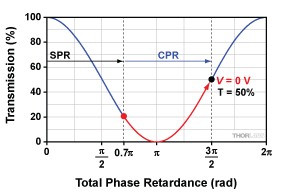
Click to Enlarge
Figure 8: The above graph shows the effect of an arbitrary SPR on the voltage transmission response. CPR is added to SPR to set a new V = 0 V operating point.
Amplitude Modulator Compensation
The SPR results in an arbitrary transmission at 0 V, yet many applications require the modulator to be set at a specific transmission point like peak (T = 100%), quadrature (T = 50%), or null (T = 0%). In such cases, we must compensate for the SPR to reach the desired operating point. This is done by adding a compensating phase retardance, CPR. Methods for adding CPR are described in the next section. There are then three components to the TPR:
TPR = SPR + VPR + CPR
Figure 8 shows the transmission function and the same arbitrary, nonzero SPR used in the previous section. In this example, we add 0.8pi of compensation to reach the quadrature operating point (i.e., TPR = 3pi/2 and T = 50% at V = 0 V). Note you can add or subtract any value of compensation to reach any desired operating point.
It should also be noted that it is often possible to create custom versions of the modulator for specific wavelength applications that do not require an adjustable compensator. Please contact Thorlabs' Tech Support to discuss this.
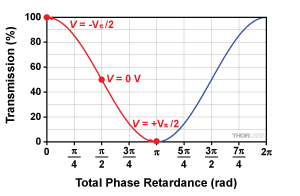
Click to Enlarge
Figure 10: Amplitude Modulator Transmission Function at a Quadrature Operating Point
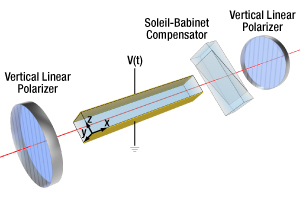
Click to Enlarge
Figure 9: Schematic of the Amplitude Modulator with Optical Compensation
Compensation Methods
If compensation is necessary to set a specific operating point for your application, then one of two main compensation methods can be employed: electrical or optical. The first method simply uses an applied DC voltage, VDC, in addition to the applied modulation voltage. In the example given in Figure 8, one must add a DC voltage of 0.8Vpi to reach the 50% transmission point. The equation for CPR then looks like this:
CPR = pi ⋅ VDC / Vpi = 0.8pi
The static DC voltage introduces an electrically tunable component to the CPR. This electrical DC compensation scheme works well at most wavelengths, but it’s worth noting that light at shorter wavelengths (400 - 600 nm) can actually produce an internal electric field that negates the applied DC electric fields.
The second method, optical compensation, however, works uniformly well at all wavelengths. For this we typically use a tunable waveplate, such as a Soleil-Babinet compensator. As shown in Figure 9, when aligned with the crystal's axes, the compensator introduces an optically tunable CPR. This is especially advantageous in the case of non-resonant amplitude modulators at long wavelengths, where extremely high voltages would be required for pure electrical compensation.
One of the benefits of optical compensation is that it can reduce the absolute voltage required for full modulation. In the AM example, setting the operating point at peak (T = 100%) or null (T = 0%) requires the full Vpi voltage to swing between a transmission minimum and a maximum. Alternatively, when the operating point is set to quadrature (T = 50%), the required voltage range becomes -Vpi/2 to +Vpi/2. This means the absolute value of the drive voltage is effectively cut in half, but it does need to be a bipolar source to allow both the addition and subtraction of VPR, as shown in Figure 10.
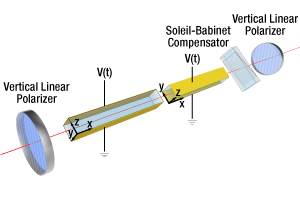
Click to Enlarge
Figure 11: Schematic of the Temperature-Compensated Amplitude Modulator with Optical Compensation
Temperature-Independent Amplitude Modulator
One of the tricky issues with LN modulators is that the crystal’s refractive indices are temperature-dependent due to the thermo-optic effect. To prevent the output polarization state from drifting with temperature, our amplitude modulators contain a second, matched crystal that is rotated by 90° with respect to the first. Figure 11 depicts this configuration. (Note: Thorlabs' PMs contain a single 40 mm long crystal, while AMs contain two 20 mm long crystals).
Each crystal independently contributes to the SPR, as given by:
TPR = SPR1 + SPR2 + VPR + CPR
where SPR1 and SPR2 are the static phase retardances introduced by the first and second crystals, respectively. Because the second crystal is rotated by 90°, its birefringent axes (y and z) are also rotated. Therefore, the SPR of the second crystal compensates for the SPR of the first. If the crystal lengths are perfectly matched, then SPR1 = -SPR2, and
TPR = VPR + CPR
In this way, the matched crystals compensate the thermal fluctuations in SPR, giving the modulator a temperature sensitivity below 0.01 rad/°C (in units of SPR per °Celsius). The matched crystals do not affect the modulation efficiency because they do not compensate the VPR, only the SPR. However, due to manufacturing constraints, there will still be some residual SPR. Even a small, μm-scale mismatch in crystal length can give an SPR anywhere from 0 to 2pi. Though the matched crystal pair gives effective thermal compensation, you will still need to use one of the compensation methods described in the previous section to set your operating point.
Click to Enlarge
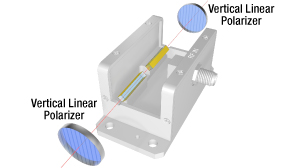
Figure 12b: Orientation of the Polarizers with Respect to the EO Modulator Housing for an Amplitude Modulator
Click to Enlarge
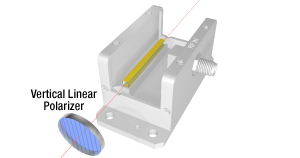
Figure 12a: Orientation of the Polarizer with Respect to the EO Modulator Housing for a Phase Modulator
Operation in the Thorlabs Housing
Figures 12a and 12b show the orientation of the LN crystals and linear polarizers with respect to the modulator housing. The EO modulators contain only an LN crystal (two for amplitude modulators) and the electronic circuit to apply the external drive voltage. They do not contain the linear polarizers or optical compensator depicted in the previous sections. Phase modulators require only an input polarizer with vertical orientation (or a polarized laser source), while amplitude modulators require both input and output polarizers.
Figure 12a depicts the standard phase modulator (PM), while Figure 12b shows the configuration of the amplitude modulator (AM). The PM crystal is the same length as two AM crystals, so the half-wave voltages for either model are similar for a given wavelength. To be more precise, PMs always have a lower Vpi than the AM equivalent because the single polarization of the phase modulator sees a higher effective EO coefficient than the net EO coefficient between two orthogonal polarizations in the amplitude modulator.
Note that the input polarizer is not needed for either version of the modulator if the laser source is already vertically linear polarized. It is also possible to run these modulators with alternate polarization schemes, but that is beyond the scope of this document. Please contact Thorlabs' Tech Support for more information.
Driving EO Modulators
Driving free-space modulators can sometimes be challenging. Our HVA200 high-voltage amplifier, which features a low-noise, ±200 V output and 1 MHz bandwidth, is ideal for driving our broadband, non-resonant EO modulators when certain operating conditions are met. The 400 V output swing allows the HVA200 to fully modulate our non-resonant AMs for wavelengths up to ~1200 nm and our non-resonant PMs across all wavelengths. The HVA200 also provides an adjustable DC bias to allow for electrical compensation to the quadrature operating point of an amplitude modulator, and effectively utilize the ±200 V bipolar output swing.
For driving non-resonant modulators at frequencies higher than 1 MHz, or at longer wavelengths, specialized amplifiers with sufficient output power, linearity, and bandwidth are required. Additionally, for non-resonant modulators, the driver should be able to drive a purely capacitive load. These devices do not present with a standard 50 Ω input impedance.
Thorlabs also provides resonant modulators that have reduced input voltage requirements. These modulators (both AM and PM) come with an internal circuit that resonates at a specific frequency. This effectively multiplies the amplitude of the external sinusoidal drive signal to the higher voltage levels the EO crystals require. The trade-off is that these modulators only operate at a specific design frequency between 1 MHz and 100 MHz. Resonant modulators that operate at 20 MHz are available from stock, but other frequencies can be requested.
Please see the full web presentation for more details about resonant and non-resonant modulators, and contact Tech Support for any more specific information or custom requests.
EO Amplitude Modulators


Click to Enlarge
Amplitude Modulator Crystal Orientation
Note: Polarizers must be purchased separately.
Our EO amplitude modulators are Pockels cell-type modulators consisting of two matched lithium niobate crystals (see the diagram to the right) packaged in a compact housing with an RF input connector. The EO crystals act as a variable waveplate with a retardance that is dependent on the applied electric field. When placed between linear polarizers, the beam intensity through the system varies with the applied voltage. See the EO Modulator Intro tab for a detailed explanation.
Please note that AM modulators operating in the -C4 band (400 - 600 nm) should only be used for AC modulation above a few Hz. MgO-doped lithium niobate can be sensitive to light in this wavelength range, displaying a slow negation to an applied DC field. The more intense the light, the faster the DC field is cancelled. Hence, in practice, a DC voltage cannot be used to bias the modulator at the desired operating point. Instead, an optical compensator can bias the modulator to the desired operating point (please see the EO Modulator Intro tab for more information on proper modulator biasing).
Part Number | Description | Price | Availability |
|---|---|---|---|
EO-AM-NR-C4 | EO Amplitude Modulator, Wavelength: 400 - 600 nm | $3,208.72 | Today |
EO-AM-NR-C1 | EO Amplitude Modulator, Wavelength: 600 - 900 nm | $3,208.72 | Today |
EO-AM-NR-C2 | EO Amplitude Modulator, Wavelength: 900 - 1250 nm | $3,208.72 | Today |
EO-AM-NR-C3 | EO Amplitude Modulator, Wavelength: 1250 - 1650 nm | $3,208.72 | Today |
EO Phase Modulators

Our EO phase modulators introduce an electrically controlled phase shift to a linearly polarized input beam. The control signal may be DC or time varying. When the control voltage is time varying, the optical beam undergoes frequency modulation. In this case, some of the energy at the fundamental optical frequency is converted into sidebands that are separated by integer multiples of the modulating frequency. The modulation depth determines the amount of energy converted into these sidebands. The graph to the right shows the relative sideband power as a function of modulation depth.
Part Number | Description | Price | Availability |
|---|---|---|---|
EO-PM-NR-C4 | EO Phase Modulator, Wavelength: 400 - 600 nm | $3,094.12 | Today |
EO-PM-NR-C1 | EO Phase Modulator, Wavelength: 600 - 900 nm | $3,094.12 | Today |
EO-PM-NR-C2 | EO Phase Modulator, Wavelength: 900 - 1250 nm | $3,094.12 | Today |
EO-PM-NR-C3 | EO Phase Modulator, Wavelength: 1250 - 1650 nm | $3,094.12 | Today |
Resonant EO Modulators

Our resonant EO modulators feature an internal, high-Q tank circuit that boosts a low-level RF input voltage to the high voltage needed to achieve full modulation depth. As a result, they can be driven by a standard laboratory function generator. a standard 20 MHz resonant amplitude modulator has a Q value of 14 and a half-wave voltage of only 15 V. By their nature, the PMs have a half-wave voltage that is approximately two-thirds that of the AMs, so a 20 MHz resonant PM will have a Vpi ~10 V.
We offer standard resonant modulators in both phase- and amplitude-modulating versions, operating at 20 MHz with a 1 MHz bandwidth. They feature a -C1 coating for use from 600 to 900 nm. Custom versions are also available, with user-specified resonant frequencies from 0.1 to 100 MHz and with any of the standard C1 - C4 AR coatings. Note that the Q value is a function of the resonant frequency and may differ considerably compared to the 20 MHz models. Please contact
Part Number | Description | Price | Availability |
|---|---|---|---|
EO-PM-R-20-C1 | Electro-Optic Resonant Phase Modulator, 20 MHz, 600 - 900 nm | $3,667.10 | Today |
EO-AM-R-20-C1 | Electro-Optic Resonant Amplitude Modulator, 20 MHz, 600 - 900 nm | $3,896.30 | Today |
Electro-Optic Modulator Glan Thompson Polarizer Mounting Adapter


Click to Enlarge
EO-PMT Polarizer Mounting Adapter
- GTH5M Mounting Adapter for Our Electro-Optic Modulators
- Easily Rotates Into and Out of Beam Path
- Ø13 mm Aperture for Use with GTH5M
- 2-56 Mounting Screw and Washer Included
The EO-PMT allows for easy interfacing of a Glan Thompson polarizer (GTH5M) to our Electro-Optic Modulators. The single mounting point allows the mount to swivel the polarizer into and out of the light path; a useful feature that allows for alignment and adjustment of the electro-optic modulators. The EO-GTH5M packages the Glan Thompson polarizer (GTH5M) with the mounting adapter.
Part Number | Description | Price | Availability |
|---|---|---|---|
EO-PMT | Glan Thompson Polarizer Mounting Adapter | $34.33 | Today |
EO-GTH5M | Glan Thompson Polarizer Mounting Adapter with GTH5M | $574.54 | Today |
EO Modulator Mounting Accessories

Our EO Modulators Can Be Mounted Using the PY005 5-Axis Stage, FT-EOMA Bracket and PY005A1 Base (Left) for a 2" (50.8 mm) Beam Height or Directly to the PY005 Stage (Right)
- Compact Platform with Five Axes of Adjustment
- Adapter Bracket Mounts Modulator to the Platform or Any FiberBench Over 70 mm Long
- PY005A1 Mounting Base Mounts EO Modulators with a 2" (50.8 mm) Nominal Beam Height when Used Together with the PY005 and FT-EOMA
- Mounting Screws Included with All Mounting Adapters
The PY005 is a compact stage with five degrees of freedom. Two actuators adjust the yaw and Y axes, two actuators adjust the pitch and Z axes, and a single actuator adjusts the X axis. Two F19SC1 locking collars are epoxied onto the yaw and Y-axis actuators, acting as hard stops so these actuators cannot be overdriven. The pitch, X-axis, and Z-axis actuators bottom out inside bores, which prevents them from being overdriven. Please note that using F19SC1 collars with the pitch, X-axis, and Z-axis actuators is not recommended, as it will reduce the overall travel range of the stage. Click here for full information about the PY005 stage.
An EO modulator can be mounted directly to the PY005 using the #8 counterbore accessible from the bottom of the stage (shown to the far right). This counterbore is accessible even when the PY005A1 base is attached to the stage. Additionally, the EO modulator can be mounted to the stage using the FT-EOMA adapter bracket (shown to the immediate right). When the FT-EOMA is used to mount the modulator and the PY005A1 mounting base is attached to the bottom of the stage, the optical axis of the EO modulator is positioned at a nominal height of 2" (50.8 mm) from the optical table.
The FT-EOMA adapter bracket can also be used to mount a Modulator onto a FiberBench. The length of the bench needs to be at least 70 mm to mount the modulator. Incorporation of the optional EO Modulator optic mount and polarizer (EO-GTH5M) will require a longer FiberBench. The Linear Polarizer modules are well suited for use with an EO Modulator in a FiberBench System. The application picture to the right shows an EO Modulator with an FT-38X100 Multi-Axis FiberBench, one Linear Polarizer, and two FiberPorts.
Part Number | Description | Price | Availability |
|---|---|---|---|
PY005/M | Compact Five-Axis Stage, 27.4 mm (1.08") Deck Height, Metric | $483.88 | Today |
PY005A1/M | Slotted Mounting Base for PY005/M 5-Axis Stage, 36.6 mm Deck Height, Metric | $32.74 | Today |
FT-EOMA | Adapter Bracket for EO Modulators and FiberBenches or PY005(/M) Stage | $61.34 | Today |
PY005 | Compact Five-Axis Stage, 27.4 mm (1.08") Deck Height | $483.88 | Today |
PY005A1 | Slotted Mounting Base for PY005 5-Axis Stage, 1.44" Deck Height | $32.74 | Today |