Mounted N-BK7 Plano-Convex Lenses (Uncoated)

- Positive Focal Length for Infinite Conjugate Applications
- Ø1/2", Ø1", Ø1.5", or Ø2" Optics in SM-Threaded Mounts
LA1256-ML
(Ø2")
LA1027-ML
(Ø1")
LA1131-ML Lens
Mounted in a KB1P
Quick-Release Mount
(KB1P Mount Sold Separately)
LA1289-ML
(Ø1/2")
LA1385-ML
(Ø1.5")

Please Wait
| N-BK7 Plano-Convex Spherical Singlets | |
|---|---|
| Lens Shape | Plano-Convex |
| Substrate Material | N-BK7 (Grade A)a |
| Wavelength Range | 350 nm - 2.0 μm (Uncoated) |
| Design Wavelength | 587.6 nm or 633 nmb |
| Index of Refraction | 1.517 (@ 587.6 nm) 1.515 (@ 633 nm) |
| Surface Quality | 40-20 Scratch-Dig |
| Surface Flatnessc (Plano Side) | λ/2 |
| Spherical Surface Powerc,d (Convex Side) |
3λ/2 |
| Surface Irregularityc (Peak to Valley) | λ/4 |
| Abbe Number | vd = 64.17 |
| Centration | <3 arcmin |
| Clear Aperture | Ø1/2" Lenses: >Ø11.05 mm Ø1" Lenses: >Ø22.86 mm Ø1.5" Lenses: >Ø34.29 mm Ø2" Lenses: >Ø45.72 mm |
| Focal Length Tolerance | ±1% |
Features
- Material: N-BK7
- Wavelength Range: 350 nm - 2.0 μm (Uncoated)
- Choose from Ø1/2", Ø1", Ø1.5", or Ø2" Optics
- Focal Lengths from 15 mm to 2500 mm
- Mounted in SM-Compatible Lens Cells with Retaining Rings
- Offers Excellent Transmission Throughout the Visible and Near Infrared
These uncoated Plano-Convex Lenses are fabricated from RoHS-compliant N-BK7. N-BK7 is typically chosen whenever the additional benefits of UV fused silica (i.e., good transmission further into the UV and a lower coefficient of thermal expansion) are not necessary. These Ø1/2", Ø1", Ø1.5", and Ø2" lenses are mounted in SM05 (0.535"-40), SM1 (1.035"-40), SM1.5 (1.535"-40), and SM2 (2.035"-40) compatible mounts, respectively, for compatibility with our line of SM-threaded lens tubes. An SM-threaded retaining ring is used to secure each lens within the mount. Each mount is engraved with the item #, lens type, focal length, and an arrow pointing toward the curved surface of the lens.
Like all plano-convex lenses, these lenses have a positive focal length and near-best-form shape for infinite and finite conjugate applications. They can be employed to converge collimated beams or collimate light from a point source. To minimize the introduction of spherical aberration, a collimated light source should be incident on the curved surface of the lens when being focused and a point light source should be incident on the planar surface when being collimated.
The focal length of each lens can be calculated using a simplified thick lens equation:

Here n is the index of refraction and R is the radius of curvature of the lens surface. For more information, please see the Tutorial tab.
Although uncoated lenses are highlighted on this page, these N-BK7 plano-convex lenses are also available with one of five antireflective coatings (-A, -AB, -B, -C, or -D), which reduce the amount of light reflected from each surface of the lens over the specified wavelength range. Links to each of these pages can be found in the selection guide table below. Please see the Graphs tab for coating information.
| N-BK7 Plano-Convex Lens Selection Guide | |
|---|---|
| Unmounted Lenses | Mounted Lenses |
| Uncoated | Uncoated |
| -A Coating (350 - 700 nm) | -A Coating (350 - 700 nm) |
| -AB Coating (400 - 1100 nm) | -AB Coating (400 - 1100 nm) |
| -B Coating (650 - 1050 nm) | -B Coating (650 - 1050 nm) |
| -C Coating (1050 - 1700 nm) | -C Coating (1050 - 1700 nm) |
| -D Coating (1650 - 3000 nm) | - |
Custom coatings are also available. Please contact Tech Sales for a quote. N-BK7 lens kits are also available. Please click here for information.
| Quick Links to Other Spherical Singlets | ||||||
|---|---|---|---|---|---|---|
| Plano-Convex | Bi-Convex | Best Form | Plano-Concave | Bi-Concave | Positive Meniscus | Negative Meniscus |
The transmission graph below is for uncoated N-BK7. It represents total transmission through a 10 mm thick, uncoated sample, and the losses within the 350 nm to 2.0 µm wavelength range are primarily due to surface reflections.
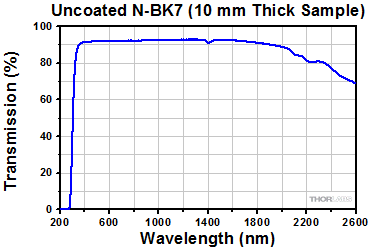
Click to Enlarge
Click Here for Raw Data
| N-BK7 Plano-Convex Lens Selection Guide | |
|---|---|
| Unmounted Lenses | Mounted Lenses |
| Uncoated | Uncoated |
| -A Coating (350 - 700 nm) | -A Coating (350 - 700 nm) |
| -AB Coating (400 - 1100 nm) | -AB Coating (400 - 1100 nm) |
| -B Coating (650 - 1050 nm) | -B Coating (650 - 1050 nm) |
| -C Coating (1050 - 1700 nm) | -C Coating (1050 - 1620 nm) |
| -D Coating (1650 - 3000 nm) | - |
The lenses sold on this page are also available with broadband antireflective coatings, the reflectance traces of which are shown in the graph below.
These high-performance multilayer AR coatings have an average reflectance of less than 0.5% (per surface) across the specified wavelength ranges (except for the -AB and -D coatings, which provide <1.0% average reflectance) and provide good performance for angles of incidence (AOI) between 0° and 30° (0.5 NA). For optics intended to be used at large incident angles, consider using a custom coating optimized at a 45° angle of incidence; this coating is effective from 25° to 52°.
The plot shown below indicates the performance of the standard coatings in this family as a function of wavelength. Broadband coatings have a typical absorption of 0.25%, which is not shown in the reflectance plots.
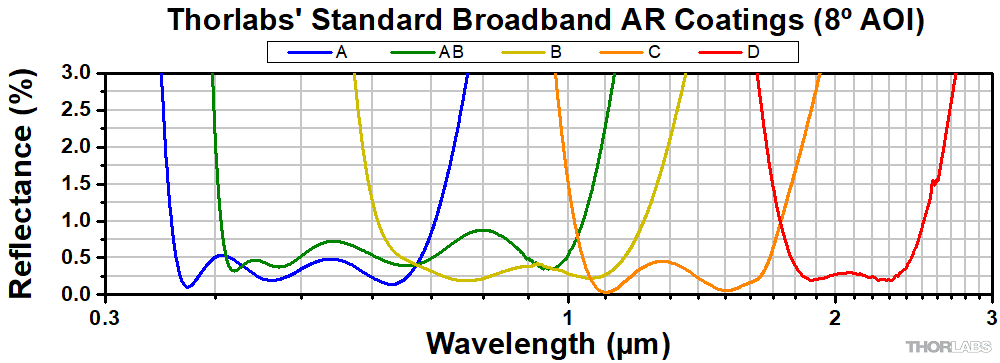
Click Here for More Information on Thorlabs' AR Coatings
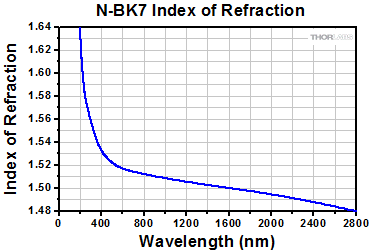
Click here for detailed substrate data.
In the thick lens equation, use the index of refraction for N-BK7 at the wavelength of interest to approximate the wavelength-dependent focal length of any of the plano-convex lenses.
The focal length of a thick spherical lens can be calculated using the thick lens equation below. In this expression, nl is the index of refraction of the lens, R1 and R2 are the radii of curvature for surfaces 1 and 2, respectively, and d is the center thickness of the lens.
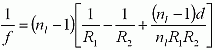
When using the thick lens equation to calculate the focal length of a plano-convex lens, R1=∞ and R2=-R. Note that the minus sign in front of R is due to the sign convention used when deriving the thick lens equations and values of R are reported in the specification tables below. Therefore, via substitution, the thick lens equation becomes:
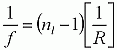
The focal length of the lens calculated using the simplified thick lens equation directly above is the distance between the second (back) principal plane (H") and the position at which a collimated beam incident on the curved surface of the plano-convex is focused. The principal plane positions of a thick lens can be calculated with the following equations:
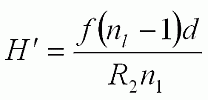 and
and 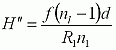
However, as with the thick lens equation, H' simplifies to zero and H" simplifies to:
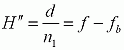
when used to calculate the principal plane locations of plano-convex lenses. fb is the back focal length of the unmounted lens, which is often referred to as the working distance. For mounted lenses, the working distance is measured from the back of the threaded housing.
| Posted Comments: | |
user
(posted 2022-10-05 19:35:25.74) Hi, I wanted to ask about the damage threshold of the uncoated lenses which seems to not be reported in the specifications. Is usually damage threshold for these higher than the coated ones?
I looked through the LIDT part for the coated lenses but there were no information for the uncoated ones.
Thanks cdolbashian
(posted 2022-10-24 09:33:01.0) Thank you for reaching out with this inquiry. For our uncoated substrates we have not done extensive damage threshold testing as the required power would be quite high. Most of these substrates will experience thermal lensing before they are damaged in earnest. I have reached out to you directly to discuss the compatibility of your optical source with our lenses. sleduc
(posted 2017-12-15 15:10:54.887) Good morning,
We bought a LA1484-ML lens.
The Radius of Curvature is 154,5mm.
Can you tell me what is the tolerance of this radius? And more, do you have a precise measure of these lenses?
Thank you.
Simon Leduc tfrisch
(posted 2017-12-15 02:01:11.0) Hello, thank you for contacting Thorlabs. The radius-of-curvature tolerance will be ±1% like the focal length tolerance. We are able to measure the focal length of individual lenses. I will reach out to you with details about this service. |




 Products Home
Products Home













 N-BK7, Mounted, Uncoated
N-BK7, Mounted, Uncoated