Noise Eaters / Laser Amplitude Stabilizers

- Laser Amplitude Stabilizer / Variable Attenuator
- Models with Wavelength Ranges Covering 425 - 1620 nm Available
- Internal Closed-Loop Feedback
Front
Back
NEL02A Noise Eater with Half-Wave Plate in CRM1T Rotation Mount
Application Idea
NEL01A
Modulation Input

Please Wait
Click to Enlarge
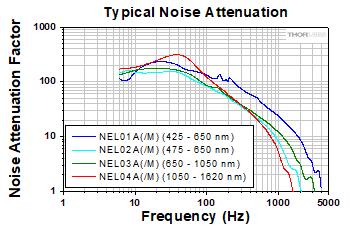
Noise attenuation factor is the ratio of noise amplitude before and after the noise eater. See the Performance tab for detailed attenuation plots.
Features
- Reduces Laser Intensity Noise
- Also Functions as a Variable Attenuator or EO Modulator
- Models for use at 425 - 650 nm, 475 - 650 nm, 650 - 1050 nm, or 1050 - 1620 nm
- Maximum Input Power of up to 1.65 W, Depending on Model, Wavelength, and Beam Size
(See the Operation Tab for Details) - Excellent for Sensitive Experiments such as Optical Tweezers
- Ideal for Stabilizing CW Lasers
Thorlabs' Liquid Crystal Noise Eaters / Laser Amplitude Stabilizers are precision instruments for stabilizing, modulating, and attenuating the power of linearly polarized light. These closed-loop systems are designed for use with light in the 425 - 650 nm [Item # NEL01A(/M)], 475 - 650 nm [Item # NEL02A(/M)], 650 - 1050 nm [Item # NEL03A(/M)], or 1050 - 1620 nm [Item # NEL04A(/M)] wavelength range. We offer noise eater models for low (<60 mW) or high (<1.65 W) power use, all with external modulation inputs. See the Specs tab for details.
Noise Reduction
Utilizing a liquid crystal amplitude modulator, combined with an internal photodiode for power measurement and a feedback control circuit, these noise eaters can eliminate intensity noise in linearly polarized light, achieving amplitude stabilization of within 0.05% of a selected output power. The input power can be set to one of several ranges using the switches on the top of the unit, which permit the noise eater to remove noise without unnecessarily attenuating the signal power. The potentiometer is then adjusted to select the output power (see the Operation tab for more information). Long-term performance and frequency characterization for each noise eater model are shown on the Performance tab.

Click for Details
NEL02A Top View Showing Power Range Adjustment Switches and Modulation Input
Click to Enlarge
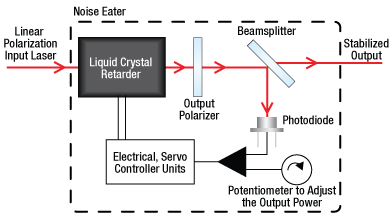
Noise Eater Block Diagram
Power Attenuation and Modulation
These noise eaters are also capable of continuously attenuating and modulating the laser output using the liquid crystal retarder and integrated polarizer. Unlike most attenuators available, Noise Eaters attenuate the laser power rapidly without the use of any mechanical components. The noise eater's attenuation capabilities can be controlled via the onboard potentiometer or electrical modulation input.
Mechanical Compatibility
Thorlabs' Noise Eaters are post mountable in two orientations via 8-32 (M4) tapped holes. They also feature 4-40 tapped holes on the front and back for 30 mm Cage System compatibility and an SM1-threaded (1.035"-40) rear aperture for Ø1" Lens Tube compatibility.
| Item # | NEL01A(/M) | NEL02A(/M) | NEL03A(/M) | NEL04A(/M) | |
|---|---|---|---|---|---|
| Wavelength Range | 425 - 650 nm | 475 - 650 nm | 650 - 1050 nm | 1050 - 1620 nm | |
| Switchable High Power Mode | - | ||||
| Noise Attenuation Performance Specs | |||||
| Output Power Stabilitya | ±0.05% (RMS) | ||||
| Noise Attenuation Frequency Rangeb | DC - 1.8 kHz | DC - 2.5 kHz | DC - 1.4 kHz | ||
| Noise Attenuation Amplitude Range | 0.1% to 50% of Input Signal | ||||
| Noise Attenuation Factorc | >150 at 10 Hz, 80 at 60 Hz 20 at 400 Hz, 4 at 1 kHz |
>150 at 10 Hz, 80 at 60 Hz 10 at 400 Hz, 1.5 at 1 kHz |
|||
| Effective Output Power Attenuation Ranged | 1 - 40 | 1 - 5 | |||
| Internal Polarizer Blocking DamageThreshold (Maximum Power Attenuation) |
1 W/cm2 | 10 W/cm2 | |||
| Attenuation Control | Onboard Potentiometer (10 Turns) or SMA Modulation Input | ||||
| Optical Specs | |||||
| Transmission (Click for Plot) | >85% at 635 nm | >80% at 635 nm | >85% at 780 nm | >85% at 1550 nm | |
| Power Level Switching | Four Position Power Range Switch | High/Low Power Mode Switch and Four Position Power Range Switch | |||
| Maximum Input Power | See the Max Powers at Various Wavelengths Section on the Operation Tab | ||||
| Minimum Input Power | 0.5 mW | ||||
| Polarization Extinction Ratio at Output | >1000:1 Over Wavelength Range | ||||
| Damage Threshold (CW)e | 0.8 W/cm2 | 8 W/cm2 | |||
| Input Aperture | Ø5 mm | ||||
| Input Beam Diameterf | Ø4 mm (Max) | ||||
| Output Beam Displacement | 1 mm Vertically (in the Direction of Input Polarization) | ||||
| Beam Divergence | 5 mrad (Max) | ||||
| Angle of Incidence | ±2° (Max) | ||||
| Input Polarization Tolerance | ±3° | ||||
| Wavefront Distortion | ≤λ/4 at 635 nm | ≤λ/2 at 635 nm | |||
| AR Coating | Ravg <0.5% from 400 - 650 nm | Ravg <0.5% from 650 - 1100 nm | Ravg <0.5% from 1050 - 1620 nm | ||
| Modulation Performance Specs | |||||
| Modulation Input | SMA Connector, 0 - 2.5 V, 10 kΩ Input Impedance | ||||
| Extinction Ratiog | 512.6 | 7.7 | 6.5 | ||
| Minimum Rise / Fall Timeh | 0.65 ms / 7.3 ms | 0.75 ms / 11.5 ms | 2.8 ms / 25 ms | ||
| Pulsed Laser Input Repetition Rate | >1 MHz | ||||
| General Specs | |||||
| Mounting Options | Two 8-32 (M4) Tapped Holes for Post Mounting 30 mm Cage System Compatible via Eight 4-40 Tapped Holes Ø1" Lens Tube Compatible via 4 mm Deep Internal SM1 Threads on Rear Side |
||||
| Operating Temperature Range | 15 °C to 45 °C | ||||
Noise Eater Performance Graphs
In the graphs below, noise attenuation was measured as one of three parameters was varied: input power level, input signal modulation (noise) amplitude, and output signal attenuation. The graphs show that the noise eaters provide consistent performance regardless of changes in these parameters.
Graph Definitions
Noise Attenuation at Various Input Power Levels
Noise attenuation factor is the ratio of noise amplitude before and after the noise eater. In these graphs, the attenuation factor was measured for several different input power levels, with a fixed signal modulation depth (noise amplitude). The graphs below show that the noise eaters provide consistent performance regardless of input power level.
Noise Attenuation at Various Input Signal Modulations
In these graphs, the input signal was modulated with a sine wave to simulate noise. The attenuation factor was measured at a variety of modulation depths (noise amplitudes). The graphs below show that the noise eater provides consistent performance even at large noise levels.
Noise Attenuation at Various Output Signal Power Levels
Since the noise eater uses a liquid crystal modulator as the optical control element, the noise attenuation is achieved by attenuating the laser beam when noise appears. Our noise eaters are carefully designed to optimize the noise attenuation performance without needing to severely attenuate the signal. These graphs demonstrate that the specified noise attenuation can be reached with a cost of only 5% - 10% overall attenuation of the output power, and further increases in attenuation does not significantly improve the noise attenuation.
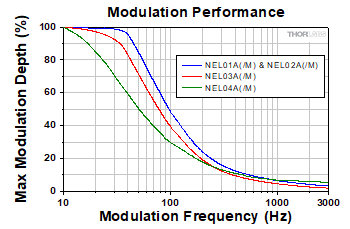
Modulation Performance
Noise eaters with a modulation input can also be used as EO modulators. In these graphs, a sine wave with a 2.5 V amplitude and an increasing frequency was used to modulate a noiseless input beam. The graphs show that the maximum modulation depth decreases with increasing modulation frequency. Further testing has demonstrated that the modulation performance is consistent for a given noise eater model, regardless of the laser beam's input power.
NEL01A(/M): Low Power Noise Eater for Visible (425 - 650 nm)
Click here to download raw data.
NEL02A(/M): High/Low Power Noise Eater for Visible (475 - 650 nm)
Click here to download raw data.
NEL03A(/M): High/Low Power Noise Eater for NIR (650 - 1050 nm)
Click here to download raw data.
NEL04A(/M): High/Low Power Noise Eater for IR (1050 - 1620 nm)
Click here to download raw data.
Noise Eater Operation
Thorlabs' Liquid Crystal Noise Eaters are precision instruments for stabilizing, attenuating, and modulating laser power. Each noise eater consists of a variable attenuator (liquid crystal wave plate and polarizer), a calibrated beamsplitter, and a servo controller to control the modulator, as depicted in the block diagram to the right.
Linearly polarized light is input into the liquid crystal retarder, which, together with the output polarizer, acts as a variable retarder. A beamsplitter then sends a small part of the beam to a feedback loop consisting of a photodiode and control servo. The servo compares the optical signal to a preset signal level and applies the appropriate adjustment voltage until the optical signal reaches the desired level.
The noise eater can also be used as a variable attenuator, even without the presence of noise. By adjusting the resistance of the potentiometer, the user can set the desired output power level.

Click to Enlarge
The Noise Eater can be post mounted in two different orientations to match the input light's direction of polarization. A CRM1T(/M) Cage Rotation Mount and four 30 mm Cage Rods can mount a half-wave plate for fine tuning the polarization alignment.
Mounting and Alignment
The noise eater is designed to work with linearly polarized input light aligned with the direction of the arrow engraved on the noise eater near the input aperture. Linearly polarized light and proper alignment of the direction of polarization are important for achieving the best results from the noise eater.
In order to minimize optical losses, the noise eater does not have an input polarizer. If the incident light is not linearly polarized, a linear polarizer must be placed before the noise eater to polarize the incident light.
If the incident light is linearly polarized but is not aligned exactly vertically or horizontally, a half-wave plate can be used before the noise eater to rotate the polarization axis. As shown in the photo to the right, the noise eater's cage mount can be used along with a CRM1T(/M) cage rotation mount to rotate the half-wave plate, thus aligning the polarization axis with the noise eater.
For post mounting, the noise eater is equipped with two 8-32 (M4) threaded holes. These holes are offset by 90° so that light with a vertical or horizontal polarization axis can be aligned with the noise eater. The four 4-40 holes on the front of the noise eater can also be used to mount the noise eater in either a horizontal or vertical orientation using the Thorlabs 30 mm Cage System.
For best performance of the noise eater, it is recommended that the beam be well centered within the input aperture. Due to the optical path inside the noise eater, the output beam will be shifted down by 1.0 mm if the noise eater is mounted vertically, as shown in the left view in the figure to the right. Similarly, the output beam will be shifted sideways by 1.0 mm if the noise eater is mounted horizontally, as shown in the right view in the figure to the right.
Click to Enlarge
In the data plotted above, a sine wave with a 2.5 V amplitude and an increasing frequency was used to modulate a noiseless input beam.

Click to Enlarge
SMA Modulation Input Jack
Modulation
There is an SMA interface at the right side of the noise eater, which can be used to modulate the attenuation of the noise eater. The modulation input has a 10 kΩ input impedance. A voltage ranging from 0 to 2.5 V can be input to modulate the output power from 0 to full output. Before modulating the output power, first turn the output power level knob clockwise to the end of its travel (minimum output power setting).
Click to Enlarge
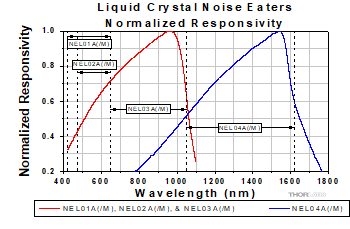
The dotted lines represent operating wavelength regions for each of the noise eaters.

Click to Enlarge
Top View Showing Power Range Adjustment Switches
Power Range Adjustment
The selection switch(es) at the top of the noise eater are used to select the input power range. The power selector should be set to the lowest value that is still higher than the actual power of the laser. For example, if the NEL01A(/M) is being used with a beam power of 8 mW at 635 nm, the selector should be set to position 3, which represents 10 mW. For specifications, refer to the Max Power tables below.
The NEL02A(/M), NEL03A(/M), and NEL04A(/M) noise eaters have two selection switches at the top of the case, which are used to select the input power range. When the low/high power switch is set to "LOW", the input power range can be set to one of the lower set of powers; when the status switch set to "HIGH", the input power range can be set to one of the higher set of powers. For specifics, refer to the Max Power tables below. Note that the NEL01A noise eater has only one selection switch.
The NEL01A(/M), NEL02A(/M), and NEL03A(/M) noise eaters use a silicon detector as part of the feedback loop, while the NEL04A noise eater uses a germanium detector. The responsivity of the detectors is different for different wavelengths, and so the power settings on the selector only correspond to the design wavelength of the detector [635 nm for Item #s NEL01A(/M) and NEL02A(/M), 780 nm for Item # NEL03A(/M), 1550 nm for Item # NEL04A(/M)]. The power range at a given wavelength is inversely proportional to the responsivity (a higher responsivity value will result in a lower power range value). The graph to the right shows the relative responsivity of both detectors at a range of wavelengths. The tables below show a rough estimate of the power settings at various wavelengths for each model.
The noise eater operates by varying how much of the signal is attenuated in order to reach the target output power and attenuate the noise. Since the noise eater can attenuate the signal but not amplify it, the clean output beam can only have a power as high as the minimum power level of the noisy signal. In practice, to remove all noise without unnecessarily attenuating the signal power, the output power level should be set to slightly lower than the minimum power of the noisy signal. See the manual for more information.
Max Powers at Various Wavelengths
The tables below list the maximum input powers for each noise eater, specified for a variety of input wavelengths and switch settings. Please note that these maximum power levels correspond to the feedback electronics of the noise eater, and in some cases, the actual maximum input power is instead limited by the damage threshold of the noise eater. For the high power noise eaters [Item #s NEL02A(/M), NEL03A(/M), and NEL04A(/M)], this damage threshold is 8 W/cm2, which corresponds to a maximum input power of 1 W if the input power is distributed evenly across the Ø4 mm clear aperture. For the low power NEL01A(/M) noise eater, the damage threshold is 0.8 W/cm2, which corresponds to a maximum input power of 100 mW if the input power is again distributed evenly across the Ø4 mm clear aperture.
| NEL01A(/M) Max Power at Various Wavelengths | |||
|---|---|---|---|
| Switch Position |
Max Power at 450 nm |
Max Power at 550 nm |
Max Power at 635 nm |
| 1 mW | 2 mW | 1.5 mW | 1 mW |
| 3 mW | 6 mW | 4.5 mW | 3 mW |
| 10 mW | 20 mW | 15 mW | 10 mW |
| 30 mW | 60 mW | 45 mW | 30 mW |
| NEL02A(/M) Max Power at Various Wavelengths | ||||
|---|---|---|---|---|
| Switch Position |
Max Power at 450 nm |
Max Power at 550 nm |
Max Power at 635 nm |
|
| L | 1 | 2 mW | 1.5 mW | 1 mW |
| L | 2 | 6 mW | 4.5 mW | 3 mW |
| L | 3 | 20 mW | 15 mW | 10 mW |
| L | 4 | 60 mW | 45 mW | 30 mW |
| H | 1 | 200 mW | 150 mW | 100 mW |
| H | 2 | 600 mWa | 450 mW | 300 mW |
| H | 3 | 1000 mWa | 750 mWa | 500 mW |
| H | 4 | N/Ab | ||
| NEL03A(/M) Max Power at Various Wavelengths | |||||||
|---|---|---|---|---|---|---|---|
| Switch Position |
Max Power at 650 nm |
Max Power at 700 nm |
Max Power at 780 nm |
Max Power at 900 nm |
Max Power at 1000 nm |
Max Power at 1100 nm |
|
| L | 1 | 1.2 mW | 1.1 mW | 1 mW | 0.9 mW | 0.9 mW | 3.3 mW |
| L | 2 | 3.5 mW | 3.3 mW | 3 mW | 2.6 mW | 2.7 mW | 10.0 mW |
| L | 3 | 11.8 mW | 11.1 mW | 10 mW | 8.8 mW | 8.9 mW | 33.3 mW |
| L | 4 | 35.5 mW | 33.3 mW | 30 mW | 26.3 mW | 26.8 mW | 100 mW |
| H | 1 | 120 mW | 111 mW | 100 mW | 86.0 mW | 89.3 mW | 333 mW |
| H | 2 | 355.5 mW | 333 mW | 300 mW | 258.0 mW | 268 mW | 999 mWa |
| H | 3 | 600 mWa | 500 mW | 500 mW | 430.0 mW | 446.6 mW | 1650 mWa |
| H | 4 | N/Ab | |||||
| NEL04A(/M) Max Power at Various Wavelengths | ||||||||
|---|---|---|---|---|---|---|---|---|
| Switch Position |
Max Power at 1050 nm |
Max Power at 1150 nm |
Max Power at 1250 nm |
Max Power at 1350 nm |
Max Power at 1450 nm |
Max Power at 1550 nm |
Max Power at 1620 nm |
|
| L | 1 | 1.9 mW | 1.6 mW | 1.4 mW | 1.2 mW | 1 mW | 1 mW | 1.6 mW |
| L | 2 | 5.8 mW | 4.8 mW | 4.1 mW | 3.5 mW | 3.1 mW | 3 mW | 4.8 mW |
| L | 3 | 19.2 mW | 16 mW | 13.7 mW | 11.7 mW | 10.4 mW | 10 mW | 16 mW |
| L | 4 | 57.6 mW | 48 mW | 41.1 mW | 35.1 mW | 31.3 mW | 30 mW | 48 mW |
| H | 1 | 190 mW | 160 mW | 137 mW | 117 mW | 104.7 mW | 100 mW | 160 mW |
| H | 2 | 500 mW | 480 mW | 411 mW | 351 mW | 313.4 mW | 300 mW | 480 mW |
| H | 3 | 835 mWa | 800 mWa | 685 mWa | 585 mWa | 520 mWa | 500 mW | 800 mWa |
| H | 4 | N/Ab | ||||||
| Posted Comments: | |
Edward Flagg
(posted 2023-07-14 20:03:53.777) I am trying to use a NEL02 as a variable attenuator controlled by the modulation voltage. For this to work, the potentiometer knob must be turned entirely clockwise (CW), otherwise the transmitted intensity will not reach the minimum value. However, if the modulation voltage is too low (maybe 6-8 mV), then when the knob is turned to the CW limit, the transmitted intensity will jump up to some mid-range value and the device stops responding to the modulation voltage input. To "reset" the behavior, the knob must be turned counter-clockwise (CCW) until the intensity increases, then it may be turned back CW again to lower the intensity.
My question is whether this behavior is purposely designed into the device, or whether it is a sign that the device is failing. For example, maybe the potentiometer needs to be replaced. If this is a design choice, is there a way to avoid it? It limits the achievable extinction ratio. cdolbashian
(posted 2023-07-21 02:50:10.0) Thank you for contacting Thorlabs. We have contacted you directly to troubleshoot this issue, as this is not intended to be the behavior of the device. Yaqing Zhang
(posted 2023-05-02 22:05:46.673) Hi, Could you please advise if NEL02A works for my pulsed laser ( >100 mW output, 514 nm center wavelength, ~250 fs pulse duration, 40 MHz rep rate) ? Thanks!
Yaqing Zhang
Michigan State University
yqz@msu.edu jdelia
(posted 2023-05-08 08:30:17.0) Thanks for contacting Thorlabs! The Noise Attenuation Frequency Range of NEL02A is DC-1.8 kHz. The response time of the NEL is much longer than the repetition period of the laser and NEL can be thought of as responding to the pulse's average power, as opposed to its peak power. The noise attenuation performance should be fine considering only the repetition rate. However, the liquid crystal material has large dispersion near 520 nm, and there are also input power limitations of NEL, our NEL might not be a suitable item for your application. Brian Wilmer
(posted 2022-12-05 13:26:56.89) There are images of plots of "Long-Term Performance." Could you provide the raw data for these?
Actually it would be nice to have a plot of signal intensity vs time resolved down to much shorter timescales such as microseconds (even if it cannot stabilize well on this time scale), ms, and seconds.
Perhaps the raw data for a minute or few seconds the users could drill into for whatever resolution they're interested in.
Thank you cdolbashian
(posted 2022-12-15 02:24:31.0) Thank you for contacting Thorlabs. The raw data can be downloaded by clicking on the download link in the upper left corner of the table (which can be found under the "Performance" tab). The sampling interval of the raw data is on the minute scale. For data on shorter time scales, in the first three entries of the table we show the noise attenuation factor as plots versus frequencies, in which the sampling frequency was a few 10kHz (with short enough time). user
(posted 2022-10-11 09:37:50.257) How well does the NEL01A work at 422 nm? I know this is close but just outside the quoted range? cdolbashian
(posted 2022-10-14 03:02:27.0) Thank you for contacting Thorlabs. The working wavelength range of NEL01A is limited by the optics inside. We have reached out to you directly to discuss your laser parameters as well as the potential option for a loan unit. user
(posted 2021-09-30 13:34:50.583) Hello,
How does the regulated CW power level depend on the temperature of the NEL03? i.e. How much can I expect the power level to fluctuate per 1°C fluctuation of the ambient? YLohia
(posted 2021-10-11 04:49:34.0) Hello, thank you for contacting Thorlabs. Please refer to the "Long-Term Noise Attenuation" plot in the "Performance" tab (raw data is available online). The temperature fluctuations could be up to 2-3 ℃. NS .
(posted 2020-08-12 06:51:16.42) I have a 15 mW He-Ne laser (Thorlabs), and I want to reduce the inherent noise (RMS: 0.5%) of this laser. How much noise can you expect if you use the NEL01 or 02 model? YLohia
(posted 2020-08-31 11:38:01.0) Hello, thank you for contacting Thorlabs. Your HeNe laser tubes is not stabilized and the noise at certain frequencies would shift with changes in temperature or other factors. The noise for this HeNe can extend into the MHz range but the NEL series is only intended to stabilize noise in the < 1 kHz range. Laerte Patera
(posted 2019-10-11 11:09:54.81) Is it possible to couple the NEL02 stabilizer
with a NPL64C (640 nm) operated at 60 kHz (pulse of 100 ns, average power: 20 mW) to stabilize intensity fluctuation in the order of seconds/minutes? YLohia
(posted 2019-10-15 08:23:16.0) Thank you for contacting Thorlabs. The NEL02 would provide optimal performance with a pulsed laser such as the NPL64C once the pulse repetition rate is significantly higher than the cut-off frequency of the NEL electronics. The NEL can therefore filter out the fluctuations from the carrier of the pulse laser. Typically, we recommend keeping a rep of rate > 1MHz, but we still expect 60kHz to be sufficient since the cut-off frequency is ~10kHz. cwong3
(posted 2019-02-10 12:46:39.713) Will this stabilizer work with a 1 kHz rep rate pulses? nbayconich
(posted 2019-03-01 11:30:18.0) Thank you for contacting Thorlabs. When the Repetition rate is less than 1MHz, the NELXX will misjudge the peak-power as noise signals and will attenuate them as well. We do not advise using a 1kHz rep rate source or a source with a repetition rate below 1Mhz as these noise eaters will not perform as expected. andrea.volpato
(posted 2019-01-31 10:10:30.217) Is it possible to couple this stabilizer with an ultrafast NOPA output 520-740 nm (30 mW, 3 KHz, 100 fs). The bandwidth is in between LCC3111H and LCC3112H specification. Which model is recommended? nbayconich
(posted 2019-02-28 09:43:44.0) Thank you for contacting Thorlabs. We have some concerns about using femto second lasers with our NEL noise eaters. There will always be broadening of the source caused by the substrate glass and LC material. The liquid crystal material has large dispersion near 520nm.
Another consideration is the laser linewidth, pico second pulses may be fine but femto second pulsed sources will likely be too wide for NEL to control. We currently don't have any performance about fs laser at the moment but we will definitely try to gather more data in the future. sdacha
(posted 2019-01-25 14:32:46.663) Can the NEL04 be used with a YAG Microchip laser at 1064 nm that produces ~1 ns pulses with a max. average power of ~140 mW (max. peak power of ~100 kW)? Does the max power in the specs correspond to max. average power or max. peak power? YLohia
(posted 2019-01-30 08:34:29.0) Hello, thank you for contacting Thorlabs. While we don't have a formal pulsed damage threshold for the NEL04, we do expect 100kW peak power to damage the device. The CW damage threshold is 8W/cm^2. gregory.hoth
(posted 2018-10-23 15:38:40.257) Is it possible to use the modulation input of these noise eaters to control the DC power level?
It would be useful to have electronic control of the power transmitted by the noise eater. nbayconich
(posted 2018-11-15 10:20:15.0) Thank you for contacting Thorlabs. Yes it is possible to modulate the input of the noise eaters in order to control the DC power level using the SMC interface, The noise eater can also be used as a variable attenuator, even without the presence of noise. A voltage ranging from 0 to 2.5 V can be input to modulate the output power as needed.
Please note that the output power cannot be modulated higher than the initial input power. The noise eater operates by varying how much of the signal is attenuated in order to reach the target output power and attenuate the noise. Since the noise eater can attenuate the signal but not amplify it, the clean output beam can only have a power as high as the minimum power level of the noisy signal. vytautas.purlys
(posted 2015-10-05 06:39:56.403) 1. Is it possible to use the noise eater for 400kHz - 80Mhz repetition rates of fs lasers? I need to stabilize the laser power for long durations (up to a few days), I don't need to stabilize the pulse-to-pulse stability.
2. How does the EO version work? Is the active element an electrooptical crystal or is it still liquid crystal based? besembeson
(posted 2015-10-13 08:33:51.0) Response from Bweh at Thorlabs USA: These are ideal for CW lasers so it should be suitable at the higher repetition rates (close to 80MHz) but may not be suitable at the lower repetition rates. Also ensure the peak powers are within the limits we specify. The EO version has the same configuration, using a liquid crystal retarder and polarizer. We use the term EO since these have a modulation input that allows system to act as an optical switch. max.ulbrich
(posted 2015-08-29 15:13:13.107) I have a 80mW, 561nm laser which has quite some fluctuations in intensity that I want to reduce. The beam diameter is 0.7mm 1/e2. Which product should I use? Can I keep the beam diameter or do I need to expand it before it passes the device?
Thanks, Max mthrossell
(posted 2015-09-10 06:04:01.0) Response from Matt at Thorlabs USA: We will contact you directly through our Germany office to discuss your application. forget
(posted 2015-06-10 16:59:04.63) What is the time response of the photodiode + amplifier ? Would the LCC3112H/M be usable on a 100 kHz laser at 1030 nm ? Thanks in advance for your answer.
Nicolas besembeson
(posted 2015-09-21 09:21:27.0) Response from Bweh at Thorlabs USA: The response time for the photodiode and amplifier is about 0.35us. The attenuation will be worse than specified so it may not be suitable. In certain cases such as lasers having spikes or step-like output power fluctuations the device may not be able to completely eliminate high frequency noise. pan
(posted 2015-04-07 07:43:26.793) Used LCC3112H on a Ti:Sa laser with 80MHz repetition rate, 800nm. Added noise eater to a beam path with 155mW max power output after the unit, tune to have 145mW output. Tested with PM100 for 10+ hours. See worse power stability with the noise eater. 10 hour drift on the order of ~3%.
Would appreciate comments/suggestions. jlow
(posted 2015-04-17 01:14:25.0) Response from Jeremy at Thorlabs: We will contact you directly to troubleshoot this. elharel
(posted 2014-08-14 13:32:15.683) Can the noise eater handle femtosecond pulses? What is the thickness of the beam splitter? I am concerned about significant dispersion caused by the device.
thanks besembeson
(posted 2014-08-21 02:54:28.0) Response from Bweh at Thorlabs USA: The damage threshold is 10MW/cm^2 peak power and 8W/cm^2 for CW. You can compare your power density to these values. Regarding the dispersion, I will followup with you by email to determine which unit you are interested in, so that I can provide you information about the thickness and dispersion. emeyersc
(posted 2013-11-08 10:13:44.257) Can the IR noise eater handle picosecond pulses from an OPO and still stabilize? What would be the damage threshold in this case (specifically, 1620 nm, 80 MHz, 3 ps)? jlow
(posted 2013-11-12 10:34:37.0) Response from Jeremy at Thorlabs: Since 80MHz is much higher than the bandwidth of the noise eater (2.5kHz), the LCC3113 should still stabilize. The damage threshold is around 10MW/cm^2 peak power and 8W/cm^2 for CW. tcohen
(posted 2012-11-12 13:05:00.0) Response from Tim at Thorlabs to Gediminas: Thank you for contacting us! A 650-1100nm edition of our noise eater is currently in the works and will be released shortly. For your review, we will contact you with more information on this new product. gediminas.dauderis
(posted 2012-11-12 02:01:19.23) Dear Sir/Madan,
Do you have some equipment like Liquid Crystal Noise Eater / Laser Stabilizer 1000 nm wavelength?
Yours Faithfully,
Gediminas Dauderis tcohen
(posted 2012-11-07 21:29:00.0) Response from Tim at Thorlabs: This is correct. The noise attenuation falls off as frequency increases in the target bandwidth to 2.5kHz for this LC design. If you would be interested in a high bandwidth design we would love to discuss this with you as a possible future customer inspired product. mlau
(posted 2012-10-31 21:15:06.233) If I'm reading the noise eater specs correctly, the attentuation falls with high frequency? Is that right? tcohen
(posted 2012-07-09 13:06:00.0) Response from Tim at Thorlabs: The Noise Eater will be released soon. We should be able to assemble a 100mW version but the max beam diameter for this version is 4mm. john.burke
(posted 2012-07-05 18:41:06.0) When will this be available? Is there any chance I could get a custom one with a larger aperature and power handling? I need about 100 mW so an aperature twice radius should be helpful. I could be willing to sacrifice bandwidth for long term stability and power handling.
Thanks! |

- NEL01A(/M) is a Low-Power Noise Eater (0.5 mW to 60 mW) with a Modulation Input and 425 - 650 nm Wavelength Range
- NEL02A(/M) is a Switchable Low/High-Power Noise Eater (0.5 mW to 1000 mW) with a Modulation Input and 475 - 650 nm Wavelength Range
 Products Home
Products Home












 Liquid Crystal Noise Eater / Laser Stabilizer
Liquid Crystal Noise Eater / Laser Stabilizer