Modified Thin-Lens Equation for Laser Light


Please Wait
Can the thin-lens equation be used with laser light?
In the case of laser light, a modified thin-lens equation that takes diffraction into account is recommended instead of the conventional thin-lens equation. The modified equation, which models the laser light as Gaussian beams, is appropriate for many single-mode and fiber-coupled laser sources. In addtion, the equation can be adapted for use when the laser light does not have a perfect Gaussian intensity profile. [1]
Click to Enlarge
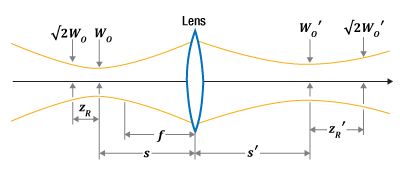
Figure 1: A thin lens, with focal length f , is shown inserted in a Gaussian beam. In the modified thin-lens equation, the object is the input beam's waist, located a distance s from the input side of the lens. The input beam's radius (W ) is Wo at its waist and maintains a similar radius over the Rayleigh range (±zR ). The image is the output beam's waist, located a distance s ' from the lens' output side. The output beam's radius (W ') is Wo' at its waist and remains nearly Wo ' over its Rayleigh range (±zR').
Click to Enlarge
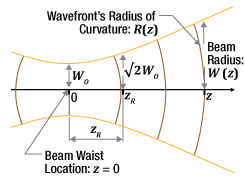
Figure 3: Gaussian beam parameters such as the radius, W(z), and the wavefront's radius of curvature, R(z), are calculated using a distance, z, referenced to the beam's waist. The waist is always located at the origin.
Click to Enlarge
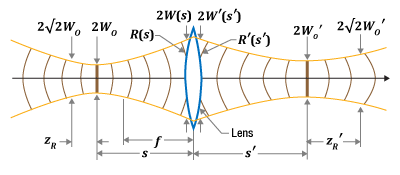
Figure 2: Key to the model are the relationships between the input and output beams at the lens. There, the beams have equal radii, and the beams' wavefront curvatures are related by the focal length of the lens. The wavefront' radius of curvature is flat (thick vertical line) at the waist and gradually becomes more spherical with increasing distance from the waist.
| Ray-Optics Thin-Lens Equation | ||||
| Conventional Thin-Lens Equation | 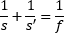 |
|||
| Gaussian Beam Equations | Lens System Relations | |||
| Beam Radius | 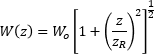 |
Beam Radii at Lens | 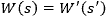 |
|
| Wavefront's Radius of Curvature |
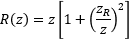 |
Wavefront Curvatures at Lens |
 |
|
| Rayleigh Range | 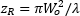 |
Magnification (m ) | 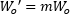 |
|
| Gaussian Beam Thin-Lens Equations | ||||
| Modified Thin-Lens Equation | Input Beam Perspective | 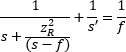 |
||
| Output Beam Perspective | 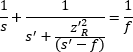 |
|||
| Magnification | 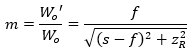 |
|||
Objects, and Images, and Laser Beams
The conventional thin-lens equation (table, top) is based on the ray optics model and uses the focal length (f ) of the lens to relate the distance
In the modified thin-lens equation, these distances refer to the separations between the lens and the input and output beam waists, respectively (Figure 1). The radius of a beam is smallest at its waist and increases with distance. A lens placed in the beam outputs a new beam with its own waist and divergence characteristics. The input beam waist radius (Wo ) is treated as the object size, and output beam waist radius (Wo' ) as the image size.
The modified thin-lens equation also includes either the input Rayleigh range
Modified Thin-Lens Equation
The incident and output light are assumed to propagate as Gaussian beams (Figure 2). The modified thin-lens equation was derived by relating the input and output beam properties (table, center) across the lens:
- The beam radii at the lens' input and output surfaces must be the same,
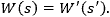
- The lens' focal length relates the radius of curvature (R ) of the wavefront incident upon the lens to the radius of curvature (R ') of the wavefront leaving the lens,
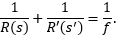
- Magnification (m ) is the ratio of the output and input beam waist radii (or diameters),
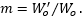
Note that the beam radius (W ) and wavefront's radius of curvature (R ) are calculated using the relative distance (z ) from the waist (Figure 3). There are two modifed thin-lens equations (table, bottom), since the form of the equation differs depending on whether the input beam parameters (zR and s ) or the output beam parameters (zR ' and s ') are known.
If the laser beam is not perfectly Gaussian, its Rayleigh range will be shorter than the Rayleigh range of an ideal Gaussian beam with the same waist radius. The ratio of the two values, M2 (M-squared), is often specified for laser beams. Multiply the beam's Rayleigh range by the M2 value, and then use this product as zR or zR ' in the modified thin-lens equation to find s ' or s , respectively.
Unique Behavior of Gaussian Beams
The behavior of Gaussian beams can be surprising, especially when compared with the predictions of the ray optics model and the conventional thin-lens equation.
For example, the conventional thin-lens equation (see table), predicts the image will appear at infinity when the object is placed at the lens' front focal point. However, for Gaussian beams, when the object beam waist is one focal length away from the input side of the lens, the image beam waist is one focal length away from the output side.
In another case, the conventional thin-lens equation predicts the image can be infinitely distant. But, if the beam is Gaussian with a nonzero Rayleigh range, the beam waist cannot be imaged to infinity. Instead, the maximum image beam waist distance,
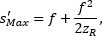
depends on the Rayleigh range of the input beam. For the image beam waist to appear at this distance, the object beam waist should be separated from the lens by a distance one Rayleigh range larger than the focal length, 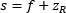 )
)
References
[1] Sidney A. Self, "Focusing of spherical Gaussian beams," Appl.Opt. 22, 658-661 (1983).
|
Looking for more Insights? |
Date of Last Edit: May 4, 2021 |
| Posted Comments: | |
| No Comments Posted |
 Products Home
Products Home Modified Thin-Lens Equation for Laser Beams
Modified Thin-Lens Equation for Laser Beams